74. Fundamental Groups of Surfaces

대수적 위상수학(algebraic topology)의 초기 성공 중 하나는 콤팩트 곡면(compact surface)을 위상동형(homeomorphism)에 따라 분류하는 문제를 해결하는 데 기여한 것이다. 이 문제를 “해결한다”는 것은, 목록에 있는 어떤 두 곡면도 서로 위상동형이 아니며 모든 콤팩트 곡면은 목록에 있는 어느 하나와 위상동형이 되는 콤팩트 곡면의 목록을 제시하는 것을 의미한다. 이것이 우리가 이 장에서 다룰 문제이다.

이 절에서는 여러 콤팩트 연결 곡면(compact connected surface)을 구성하는 방법을 보이고, 그들의 기본군(fundamental group)을 계산한다. 우리는 이 곡면들을 각각 평면의 다각형 영역(polygonal region)에서 “그 변들을 함께 붙여서” 얻은 몫공간(quotient space)으로 구성할 것이다.

이 붙이는 과정을 형식적으로 다루려면 약간의 주의가 필요하다. 먼저, 우리가 “평면의 다각형 영역”이라고 부를 것이 무엇인지 정확하게 정의하자. 평면 ${\mathbb{R}}^2$의 한 점 $c$와 양수 $a>0$이 주어졌을 때, 중심이 $c$이고 반지름이 $a$인 원을 생각하자. $n\ge 3$이고 ${\theta }_n={\theta }_0+2\pi$인 유한 수열 ${\theta }_0<{\theta }_1<\cdots <{\theta }_n$이 주어졌을 때, 이 원 위에 놓인 점들 $p_i=c+a(\cos {\theta }_i,\sin {\theta }_i)$를 생각하자. 이 점들은 원 주위를 반시계 방향으로 번호가 매겨져 있고, $p_n=p_0$이다. $p_{i-1}$과 $p_i$를 통과하는 직선은 평면을 두 개의 닫힌 반평면(closed half-plane)으로 나눈다. $H_i$를 모든 점 $p_k$를 포함하는 반평면이라고 하자. 그러면 공간

$$P=H_1\cap \cdots \cap H_n$$

은 점 $p_i$들에 의해 결정되는 다각형 영역(polygonal region) 이라 불린다. 점 $p_i$는 $P$의 꼭짓점(vertex)이라 불리고, $p_{i-1}$과 $p_i$를 잇는 선분은 $P$의 변(edge)이라 불린다. $P$의 변들의 합집합은 $\text{Bd }P$로 표기하고, $P-\text{Bd }P$는 $\text{Int }P$로 표기한다. 만약 $p$가 $\text{Int }P$의 임의의 점이라면, $P$는 $p$와 $\text{Bd }P$의 점들을 잇는 모든 선분들의 합집합이며, 두 개의 그러한 선분은 오직 점 $p$에서만 교차한다는 것을 보이는 것은 어렵지 않다.

${\mathbb{R}}^2$에 있는 선분 $L$이 주어졌을 때, $L$의 방향(orientation) 은 단순히 그 끝점들의 순서를 정하는 것이다. 첫 번째 점, $a$는 방향이 주어진 선분의 시작점(initial point)이라 불리고, 두 번째 점 $b$는 끝점(final point)이라 불린다. 우리는 종종 $L$이 $a$에서 $b$로 방향이 주어졌다고 말하며, $a$에서 $b$를 향하는 화살표를 $L$ 위에 그려서 방향을 나타낸다. 만약 $L^{\prime }$이 $c$에서 $d$로 방향이 주어진 또 다른 선분이라면, $L$에서 $L^{\prime }$으로의 양의 선형 사상(positive linear map)은 $L$의 점 $x=(1-s)a+sb$를 $L^{\prime }$의 점 $h(x)=(1-s)c+sd$로 보내는 위상동형사상 $h$이다.

만약 두 다각형 영역 $P$와 $Q$가 각각 꼭짓점 $p_0,\dots ,p_n$과 $q_0,\dots ,q_n$을 가지고, $p_0=p_n$이고 $q_0=q_n$이라면, $p_{i-1}$에서 $p_i$까지의 선분을 $q_{i-1}$에서 $q_i$까지의 선분으로 양의 선형 사상을 통해 보내는 $\text{Bd }P$와 $\text{Bd }Q$ 사이의 명백한 위상동형사상 $h$가 존재한다. 만약 $p$와 $q$가 각각 $\text{Int }P$와 $\text{Int }Q$의 고정된 점이라면, 이 위상동형사상은 $p$에서 $\text{Bd }P$의 점 $x$까지의 선분을 $q$에서 $h(x)$까지의 선분으로 선형적으로 사상함으로써 $P$와 $Q$ 사이의 위상동형사상으로 확장될 수 있다.

정의

평면의 다각형 영역 $P$가 주어졌다고 하자. $P$의 변들의 라벨링(labelling)은 $P$의 변들의 집합에서 라벨(label)이라 불리는 집합 $S$로 가는 사상이다. $P$의 각 변의 방향이 주어지고, $P$의 변들의 라벨링이 주어졌을 때, 우리는 $P$의 점들 위에 다음과 같은 동치 관계(equivalence relation)를 정의한다: $\text{Int }P$의 각 점은 오직 자기 자신과만 동치이다. 같은 라벨을 가진 $P$의 임의의 두 변이 주어졌을 때, 하나를 다른 하나 위로 보내는 양의 선형 사상을 $h$라 하고, 첫 번째 변의 각 점 $x$를 두 번째 변의 점 $h(x)$와 동치라고 정의한다. 이 관계는 $P$ 위에 동치 관계를 생성한다. 이 동치 관계로부터 얻은 몫공간 $X$는 주어진 방향과 라벨링에 따라 $P$의 변들을 붙여서 얻어졌다고 말한다.

예제 1

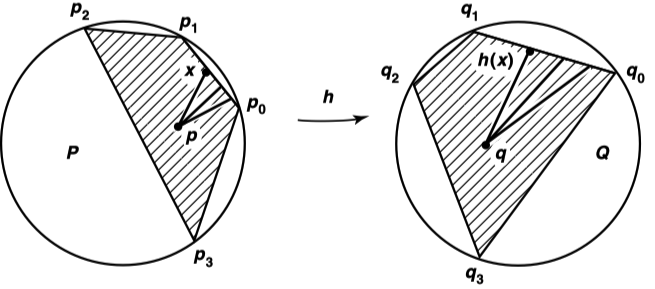
그림에 나타난 삼각형 영역의 변들의 방향과 라벨링을 생각해보자. 이 그림은 결과로 나오는 몫공간이 단위 공(unit ball)과 위상동형임을 보이는 방법을 나타낸다.

예제 2

그림에 나타난 정사각형의 변들의 방향과 라벨링은 구면 $S^2$과 위상동형인 공간을 만든다.

이제 우리는 그림을 그리지 않고 다각형 영역의 변들의 방향과 라벨을 명시하는 편리한 방법을 설명한다.

정의

$P$를 연속적인 꼭짓점 $p_0,\dots ,p_n$ ($p_0=p_n$)을 가진 다각형 영역이라 하자. $P$의 변들의 방향과 라벨링이 주어졌을 때, $a_1,\dots ,a_m$을 $P$의 변들에 할당된 서로 다른 라벨들이라 하자. 각 $k$에 대해, $a_{i_k}$를 변 $p_{k-1}{p}_k$에 할당된 라벨이라 하고, 이 변에 할당된 방향이 $p_{k-1}$에서 $p_k$로 가는 것이면 ${ϵ}_k=+1$, 그 반대이면 ${ϵ}_k=-1$이라 하자. 그러면 $P$의 변의 개수, 변의 방향, 그리고 라벨링은 기호

$$w=(a_{i_1}{)}^{{ϵ}_1}(a_{i_2}{)}^{{ϵ}_2}\dots (a_{i_n}{)}^{{ϵ}_n}$$

에 의해 완전히 명시된다. 우리는 이 기호를 $P$의 변들에 대한 길이 $n$의 라벨링 계획(labelling scheme)이라 부른다. 이것은 단순히 지수 $+1$ 또는 $-1$을 가진 라벨들의 수열이다.

우리는 보통 라벨링 계획을 제시할 때 $+1$인 지수는 생략한다. 그러면 예제 1의 방향과 라벨링은, 만약 우리가 삼각형의 위 꼭짓점을 $p_0$로 잡는다면, 라벨링 계획 $a^{-1}ba$로 명시될 수 있다. 만약 다른 꼭짓점 중 하나를 $p_0$로 잡는다면, 우리는 라벨링 계획 $ba{a}^{-1}$ 또는 $a{a}^{-1}b$ 중 하나를 얻는다.

유사하게, 예제 2에 나타난 방향과 라벨링은 (만약 우리가 정사각형의 왼쪽 아래 모서리에서 시작한다면) 기호 $a{a}^{-1}b{b}^{-1}$로 명시될 수 있다.

라벨링 계획에서 항들의 순환 순열(cyclic permutation)은 그 계획을 사용하여 형성된 공간 $X$를 위상동형에 따라 바꾸지 않는다는 것이 명백하다. 나중에 우리는 공간 $X$를 위상동형에 따라 바꾸지 않는 라벨링 계획에 가할 수 있는 다른 수정 사항들을 고려할 것이다.

예제 3

우리는 이미 토러스(torus)가 몫사상 $p\times p:I\times I\to S^1\times S^1$을 통해 단위 정사각형의 몫공간으로 표현될 수 있음을 보였다. 이 동일한 몫공간은 그림에 나타난 정사각형 변들의 방향과 라벨링에 의해 명시될 수 있다. 이것은 또한 계획 $ab{a}^{-1}{b}^{-1}$에 의해 명시될 수 있다.

예제 4

사영평면(projective plane) $P^2$는 각 $x\in S^1$에 대해 $x$와 $-x$를 동일시하여 단위 공 $B^2$로부터 얻은 몫공간과 위상동형이다. 단위 정사각형은 단위 공과 위상동형이므로, 이 공간은 또한 그림에 나타난 단위 정사각형 변들의 방향과 라벨링에 의해 명시될 수 있다. 이것은 계획 $abab$에 의해 명시될 수 있다.

이제 변들을 붙여 공간을 형성할 때 하나의 다각형 영역에만 국한될 이유가 없다. 서로소인 다각형 영역들의 유한 집합 $P_1,\dots ,P_k$와 그 변들의 방향 및 라벨링이 주어졌을 때, 하나의 영역에서와 똑같은 방식으로 변들을 붙여 몫공간 $X$를 형성할 수 있다. 또한, 방향과 라벨링은 $k$개의 라벨링 계획을 통해 유사한 방식으로 명시된다. 특정한 계획에 따라, 얻어지는 공간 $X$는 연결일 수도 있고 아닐 수도 있다.

예제 5

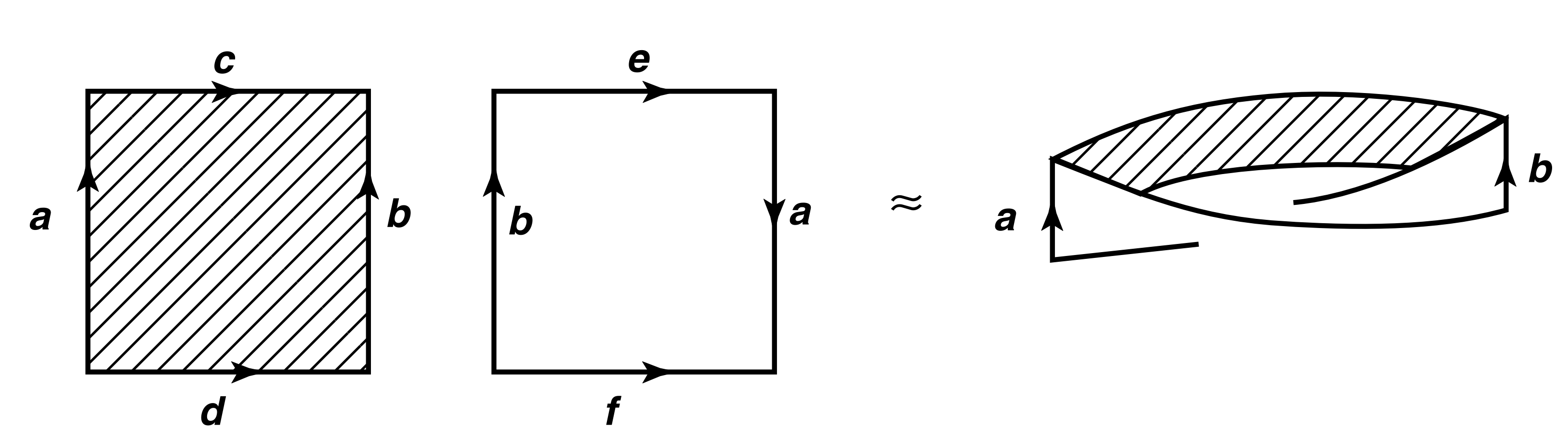
그림은 두 개의 정사각형 변들의 라벨링을 보여주며, 그 결과로 나오는 몫공간은 연결이다. 이 공간은 뫼비우스 띠(Möbius band)라 불린다. 물론, 이 공간은 라벨링 계획 $abac$를 사용하여 하나의 정사각형으로부터 얻어질 수도 있으며, 이는 확인할 수 있다.

예제 6

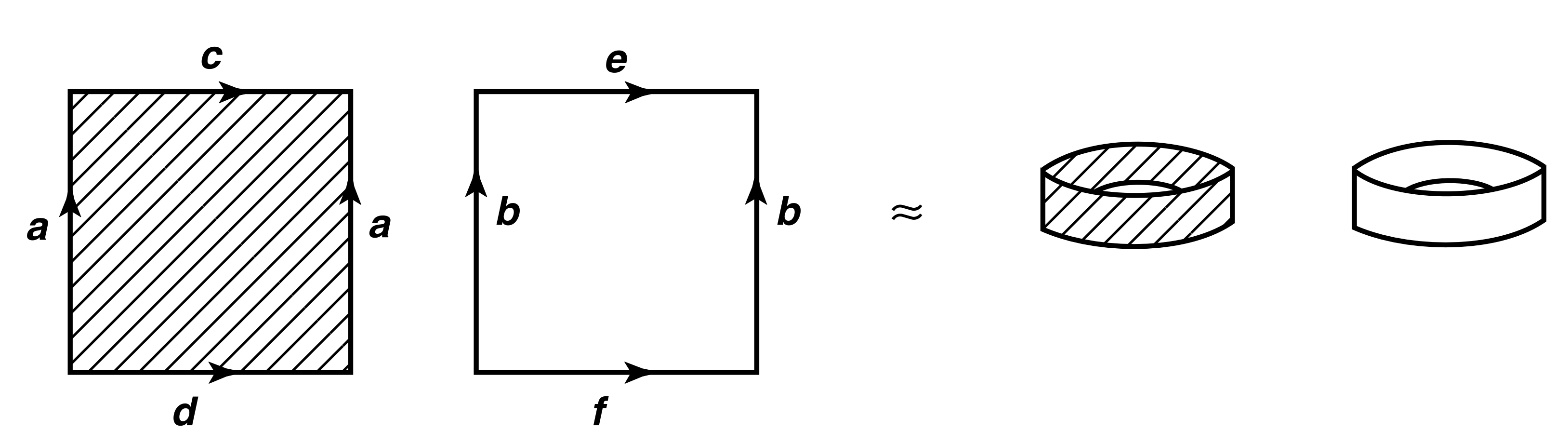
그림은 두 개의 정사각형에 대한 라벨링 계획을 보여주며, 그 결과로 나오는 몫공간은 연결이 아니다.

정리 74.1

어떤 라벨링 계획에 따라 유한 개의 다각형 영역들의 변들을 붙여서 얻은 공간 $X$는 콤팩트 하우스도르프 공간이다.

증명

단순화를 위해, $X$가 하나의 다각형 영역으로부터 형성된 경우를 다룬다. 일반적인 경우는 유사하다. 몫사상이 연속이므로 $X$가 콤팩트인 것은 자명하다. $X$가 하우스도르프임을 보이기 위해서는 몫사상 $\pi$가 닫힌 사상(closed map)임을 보이는 것으로 충분하다. (보조정리 73.3 참조) 이를 위해, 우리는 $P$의 각 닫힌 집합 $C$에 대해, 집합 ${\pi }^{-1}\pi (C)$가 $P$에서 닫혀 있음을 보여야 한다. 그러면 몫 위상의 정의에 따라 $\pi (C)$가 $X$에서 닫혀 있다는 결론이 나온다.

이제 ${\pi }^{-1}\pi (C)$는 $C$의 점들과 $\pi$ 사상에 의해 $C$의 점들에 붙여지는 $P$의 모든 점들로 구성된다. 이 점들은 결정하기 쉽다. $P$의 각 변 $e$에 대해, $C_e$를 $P$의 콤팩트 부분공간 $C\cap e$라 하자. 만약 $e_i$가 $e$에 붙여지는 $P$의 변이고 $h_i:e_i\to e$가 붙이는 위상동형사상이라면, 집합 $D_e={\pi }^{-1}\pi (C)\cap e$는 공간 $h_i(C_{e_i})$를 포함한다. 실제로, $D_e$는 $C_e$와 $e$에 붙여지는 $P$의 모든 변 $e_i$에 대한 공간 $h_i(C_{e_i})$들의 합집합과 같다. 이 합집합은 콤팩트이므로 $e$와 $P$에서 닫혀있다.

${\pi }^{-1}\pi (C)$가 집합 $C$와 $P$의 모든 변 $e$에 대한 집합 $D_e$들의 합집합이므로, 이는 $P$에서 닫혀있다.

이제 $X$가 다각형 영역의 변들을 붙여서 얻어졌을 때, 몫사상 $\pi$가 다각형 영역의 모든 꼭짓점을 $X$의 한 점으로 사상할 수도 있고, 그렇지 않을 수도 있음을 주목하자. 예제 3의 토러스의 경우, 몫사상은 이 조건을 만족시키는 반면, 예제 1과 2의 공과 구의 경우에는 그렇지 않다. 우리는 $\pi$가 이 조건을 만족시킬 때 특히 기쁜데, 이 경우 $X$의 기본군을 쉽게 계산할 수 있기 때문이다.

정리 74.2

$P$를 다각형 영역이라 하고,

$$w=(a_{i_1}{)}^{{ϵ}_1}\dots (a_{i_n}{)}^{{ϵ}_n}$$

을 $P$의 변들에 대한 라벨링 계획이라 하자. $X$를 그 결과로 나오는 몫공간이라 하고, $\pi :P\to X$를 몫사상이라 하자. 만약 $\pi$가 $P$의 모든 꼭짓점을 $X$의 한 점 $x_0$로 사상하고, $a_1,\dots ,a_k$가 라벨링 계획에 나타나는 서로 다른 라벨들이라면, ${\pi }_1(X,x_0)$는 $k$개의 생성원 ${\alpha }_1,\dots ,{\alpha }_k$를 갖는 자유군(free group)을 원소

$$({\alpha }_{i_1}{)}^{{ϵ}_1}\dots ({\alpha }_{i_n}{)}^{{ϵ}_n}$$

을 포함하는 최소 정규 부분군(least normal subgroup)으로 나눈 몫군과 동형이다.

증명

증명은 §73에서 토러스에 대해 제시한 증명과 유사하다. $\pi$가 $P$의 모든 꼭짓점을 $X$의 한 점으로 사상하므로, 공간 $A=\pi (\text{Bd }P)$는 $k$개의 원들의 쐐기(wedge of k circles)이다. 각 $i$에 대해, $a_i$로 라벨링된 $P$의 한 변을 선택하자. $f_i$를 $I$에서 반시계 방향으로 방향이 주어진 이 변 위로의 양의 선형 사상이라 하고, $g_i=\pi \circ f_i$라 하자. 그러면 루프 $g_1,\dots ,g_k$는 ${\pi }_1(A,x_0)$에 대한 자유 생성원 집합을 나타낸다. $\text{Bd }P$를 반시계 방향으로 한 번 도는 루프 $f$는 ${\pi }_1(\text{Bd }P,p)$를 생성하고, 루프 $\pi \circ f$는 루프

$$(g_{i_1}{)}^{{ϵ}_1}\ast \cdots \ast (g_{i_n}{)}^{{ϵ}_n}$$

와 같다. 이제 정리는 정리 72.1로부터 나온다.

정의

$4n$각형 영역 $P$로부터 라벨링 계획

$$(a_1{b}_1{a}_1^{-1}{b}_1^{-1})(a_2{b}_2{a}_2^{-1}{b}_2^{-1})\dots (a_n{b}_n{a}_n^{-1}{b}_n^{-1})$$

에 의해 얻어지는 공간을 생각하자. 이 공간은 토러스의 $n$겹 연결합($n$-fold connected sum of tori), 또는 간단히 $n$겹 토러스($n$-fold torus)라 불리며, $T\#\dots \#T$로 표기된다.

2겹 토러스는 위의 그림에 나타나 있다. 만약 우리가 표시된 선 $c$를 따라 다각형 영역 $P$를 나누면, 결과로 나오는 각 조각은 열린 원판이 제거된 토러스를 나타낸다. 만약 이 조각들을 곡선 $c$를 따라 붙이면, §60에서 소개하고 이중 토러스(double torus)라고 불렀던 공간을 얻는다. 유사한 논증으로 3겹 토러스 $T\#T\#T$는 아래 그림의 곡면으로 그려질 수 있음을 보인다.

정리 74.3

$X$를 $n$겹 토러스라 하자. 그러면 ${\pi }_1(X,x_0)$는 $2n$개의 생성원 ${\alpha }_1,{\beta }_1,\dots ,{\alpha }_n,{\beta }_n$을 갖는 자유군을 원소

$$[{\alpha }_1,{\beta }_1][{\alpha }_2,{\beta }_2]\dots [{\alpha }_n,{\beta }_n]$$

을 포함하는 최소 정규 부분군으로 나눈 몫군과 동형이다. 여기서 $[\alpha ,\beta ]=\alpha \beta {\alpha }^{-1}{\beta }^{-1}$는 평소와 같다.

증명

정리 74.2를 적용하기 위해서는, $X$에 대한 라벨링 계획 하에서 다각형 영역의 모든 꼭짓점이 같은 동치류에 속한다는 것을 보여야 한다. 이것은 여러분에게 맡긴다.

정의

$m>1$이라 하자. 평면의 $2m$각형 영역 $P$로부터 라벨링 계획

$$(a_1{a}_1)(a_2{a}_2)\dots (a_m{a}_m)$$

에 의해 얻어지는 공간을 생각하자. 이 공간은 사영평면의 $m$겹 연결합($m$-fold connected sum of projective planes), 또는 간단히 $m$겹 사영평면($m$-fold projective plane)이라 불리며, $P^2\#\dots \#P^2$로 표기된다.

2겹 사영평면 $P^2\#P^2$는 그림에 나타나 있다. 이 그림은 이 공간이 두 개의 사영평면 복사본에서 각각 열린 원판을 제거하고, 남은 조각들을 제거된 원판의 경계를 따라 붙여서 어떻게 얻어지는지를 보여준다.¹ $P^2$ 자체와 마찬가지로, $m$겹 사영평면은 ${\mathbb{R}}^3$에 매장될 수 없기 때문에 ${\mathbb{R}}^3$의 곡면으로 그릴 편리한 방법이 없다. 그러나 때로는 그것이 자신과 교차하는 ${\mathbb{R}}^3$의 곡면으로 그릴 수 있다. (이 경우 우리는 매장된(imbedded) 곡면이 아니라 몰입된(immersed) 곡면이라고 말한다.) 우리는 이 주제를 연습문제에서 탐구할 것이다.

정리 74.4

$X$를 $m$겹 사영평면이라 하자. 그러면 ${\pi }_1(X,x_0)$는 $m$개의 생성원 ${\alpha }_1,\dots ,{\alpha }_m$을 갖는 자유군을 원소

$$({\alpha }_1{)}^2({\alpha }_2{)}^2\dots ({\alpha }_m{)}^2$$

을 포함하는 최소 정규 부분군으로 나눈 몫군과 동형이다.

증명

$X$에 대한 라벨링 계획 하에서 다각형 영역의 모든 꼭짓점이 같은 동치류에 속한다는 것을 확인하기만 하면 된다. 이것은 여러분에게 맡긴다.

콤팩트 곡면을 형성하는 다른 많은 방법들이 존재한다. 예를 들어, $P^2$와 $T$ 각각에서 열린 원판을 제거하고, 남은 공간들을 제거된 원판들의 경계를 따라 붙일 수 있다. 이 공간이 라벨링 계획 $aabc{b}^{-1}{c}^{-1}$에 의해 6각형 영역으로부터 얻어질 수 있음을 확인할 수 있다. 하지만 우리는 이 지점에서 멈출 것이다. 왜냐하면 우리가 이미 콤팩트 연결 곡면의 완전한 목록을 얻었기 때문이다. 이것이 곡면에 대한 기본 분류 정리(basic classification theorem for surfaces)이며, 우리는 곧 이를 고려할 것이다.

Footnotes

1. klein bottle와 위상동형이다. ↩