73. The Fundamental Groups of the Torus and the Dunce Cap

우리는 이제 이전 절의 결과를 적용하여 두 개의 기본군을 계산하는데, 하나는 이미 알고 있는 것이고 다른 하나는 그렇지 않은 것이다. 여기에 포함된 기법들은 나중에 중요하게 사용될 것이다.

정리 73.1

원환면(torus)의 기본군은 두 개의 생성원(generator) $\alpha ,\beta$와 단일 관계식(relation) $\alpha \beta {\alpha }^{-1}{\beta }^{-1}$으로 구성된 표시(presentation)를 갖는다.

증명

$X=S^1\times S^1$를 원환면이라 하고, 표준 덮개 사상(standard covering map) $p\times p:\mathbb{R}\times \mathbb{R}\to S^1\times S^1$을 제한하여 얻은 $h:I^2\to X$를 생각하자. $p$를 $\text{Bd }{I}^2$의 점 $(0,0)$이라 하고, $a=h(p)$라 하며, $A=h(\text{Bd }{I}^2)$라 하자. 그러면 정리 72.1의 가설이 만족된다.

공간 $A$는 두 원의 쐐기(wedge of two circles)이므로, $A$의 기본군은 자유군(free group)이다. 실제로, $I^2$에서 경로 $a_0(t)=(t,0)$과 $b_0(t)=(0,t)$를 생각하면, 경로 $\alpha =h\circ a_0$와 $\beta =h\circ b_0$는 $A$에서 $[\alpha ]$와 $[\beta ]$가 ${\pi }_1(A,a)$의 자유 생성원계(system of free generators)를 이루는 고리(loop)이다.

이제 $I^2$에서 경로 $a_1(t)=(t,1)$과 $b_1(t)=(1,t)$를 생각하자. $\text{Bd }{I}^2$에서 다음 방정식으로 정의된 고리 $f$를 생각하자.

$$f=a_0\ast (b_1\ast ({\bar{a}}_1\ast {\bar{b}}_0)).$$

그러면 $f$는 ${\pi }_1(\text{Bd }{I}^2,p)$의 생성원을 나타내고, 고리 $g=h\circ f$는 곱 $\alpha \ast (\beta \ast (\bar{\alpha }\ast \bar{\beta }))$와 같다. 정리 72.1은 ${\pi }_1(X,a)$가 자유 생성원 $[\alpha ]$와 $[\beta ]$ 위의 자유군을 원소 $[\alpha ][\beta ][\alpha {]}^{-1}[\beta {]}^{-1}$를 포함하는 가장 작은 정규 부분군(least normal subgroup)으로 나눈 몫(quotient)임을 알려준다.

보조정리 73.2

원환면의 기본군은 랭크(rank) 2인 자유 아벨 군(free abelian group)이다.

증명

$G$를 생성원 $\alpha ,\beta$ 위의 자유군이라 하고, $N$을 원소 $\alpha \beta {\alpha }^{-1}{\beta }^{-1}$를 포함하는 가장 작은 정규 부분군이라 하자. 이 원소는 교환자(commutator)이므로, $N$은 $G$의 교환자 부분군(commutator subgroup) $[G,G]$에 포함된다. 다른 한편으로, $G/N$은 아벨(abelian)이다. 왜냐하면 이는 잉여류(coset) $\alpha N$과 $\beta N$에 의해 생성되고, $G/N$의 이 원소들은 교환되기 때문이다. 따라서 $N$은 $G$의 교환자 부분군을 포함한다.

정리 69.4에 의해 $G/N$은 랭크 2인 자유 아벨 군이다.

정의

$n$을 $n>1$인 양의 정수라 하자. $S^1$에서 $S^1$로의 회전(rotation) $r$을 각도 $2\pi /n$만큼 회전하는 것으로, 점 $(\cos \theta ,\sin \theta )$를 점 $(\cos (\theta +2\pi /n),\sin (\theta +2\pi /n))$으로 보내는 것으로 정의하자. 단위 공(unit ball) $B^2$에서 $S^1$의 각 점 $x$를 점 $r(x),r^2(x),\dots ,r^{n-1}(x)$와 동일시하여 몫공간(quotient space) $X$를 형성한다. 우리는 $X$가 콤팩트 하우스도르프 공간(compact Hausdorff space)임을 보일 것이며, 이를 n-겹 바보 모자(n-fold dunce cap) 이라 부른다.

$\pi :B^2\to X$를 몫 사상(quotient map)이라 하자. 우리는 $\pi$가 닫힌 사상(closed map)임을 보인다. 이를 위해, $B^2$의 닫힌 집합 $C$에 대해 ${\pi }^{-1}\pi (C)$ 역시 $B^2$에서 닫혀 있음을 보여야 한다; 그러면 몫 위상(quotient topology)의 정의에 의해 $\pi (C)$가 $X$에서 닫혀 있다는 결론이 나온다. $C_0=C\cap S^1$이라 하자; 이것은 $B^2$에서 닫혀 있다. 집합 ${\pi }^{-1}\pi (C)$는 $C$와 집합 $r(C_0),r^2(C_0),\dots ,r^{n-1}(C_0)$의 합집합과 같다. 이들 각각은 $r$이 동형사상(homeomorphism)이므로 $B^2$에서 닫혀 있다. 따라서 ${\pi }^{-1}\pi (C)$는 $B^2$에서 닫혀 있다.

$\pi$가 연속이므로, $X$는 콤팩트(compact)이다. $X$가 하우스도르프라는 사실은 §31의 연습문제로 주어진 다음 보조정리의 결과이다.

보조정리 73.3

$\pi :E\to X$를 닫힌 몫 사상이라 하자. 만약 $E$가 정규(normal) 공간이면, $X$도 그렇다.

증명

$E$가 정규라고 가정하자. $X$에서 한 점 집합(one-point set)은 닫혀 있는데, 이는 $E$에서 한 점 집합이 닫혀 있기 때문이다. 이제 $A$와 $B$를 $X$의 서로소인 닫힌 집합이라 하자. 그러면 ${\pi }^{-1}(A)$와 ${\pi }^{-1}(B)$는 $E$의 서로소인 닫힌 집합이다. 각각 ${\pi }^{-1}(A)$와 ${\pi }^{-1}(B)$를 포함하는 서로소인 열린 집합 $U$와 $V$를 선택하자. $\pi (U)$와 $\pi (V)$가 우리가 찾는 $A$와 $B$에 대한 열린 집합이라고 가정하고 싶지만, 그렇지 않다. 왜냐하면 이들은 열려 있을 필요도 없고($\pi$가 반드시 열린 사상은 아니다), 서로소일 필요도 없기 때문이다!

그래서 우리는 다음과 같이 진행한다: $C=E-U$라 하고 $D=E-V$라 하자. $C$와 $D$는 $E$의 닫힌 집합이므로, $\pi (C)$와 $\pi (D)$는 $X$에서 닫혀 있다. $C$는 ${\pi }^{-1}(A)$의 어떤 점도 포함하지 않으므로, $\pi (C)$는 $A$와 서로소이다. 그러면 $U_0=X-\pi (C)$는 $A$를 포함하는 $X$의 열린 집합이다. 유사하게, $V_0=X-\pi (D)$는 $B$를 포함하는 $X$의 열린 집합이다. 더욱이, $U_0$와 $V_0$는 서로소이다. 만약 $x\in U_0$이면, ${\pi }^{-1}(x)$는 $C$와 서로소이므로 $U$에 포함된다. 유사하게, $x\in V_0$이면, ${\pi }^{-1}(x)$는 $V$에 포함된다. $U$와 $V$가 서로소이므로, $U_0$와 $V_0$도 서로소이다.

2-겹 바보 모자(2-fold dunce cap)은 우리가 전에 보았던 공간, 즉 사영 평면(projective plane) $P^2$와 동형임을 주목하자. 이 사실을 확인하기 위해, $P^2$는 각 점 $x$를 그 대척점(antipodal point) $-x$와 동일시하여 $S^2$로부터 얻은 몫공간으로 정의되었음을 상기하자. $p:S^2\to P^2$를 몫 사상이라 하자. 방정식

$$i(x,y)=(x,y,(1-x^2-y^2{)}^{1/2})$$

로 주어진 $B^2$와 $S^2$의 위쪽 반구(upper hemisphere) 사이의 표준 동형사상 $i$를 취하고, 이어서 사상 $p$를 적용하자. 우리는 연속이고, 닫혀 있으며, 전사인 사상 $\pi :B^2\to P^2$를 얻는다. $\text{Int }B$에서는 단사이고, $S^1$의 각 점 $x$에 대해 $x$와 $-x$를 같은 점으로 보낸다. 따라서 이는 2-겹 바보 모자과 $P^2$ 사이의 동형사상을 유도한다.

n-겹 바보 모자의 기본군은 $P^2$에 대한 우리의 계산으로부터 예상할 수 있는 바로 그것이다.

정리 73.4

n-겹 바보 모자의 기본군은 위수(order) n인 순환군(cyclic group)이다.

증명

$h:B^2\to X$를 몫 사상이라 하자, 여기서 $X$는 n-겹 바보 모자이다. $A=h(S^1)$라 하자. $p=(1,0)\in S^1$이라 하고 $a=h(p)$라 하자. 그러면 $h$는 $p$에서 $r(p)$로 가는 $S^1$의 호(arc) $C$를 $A$ 위로 보내고, $C$의 양 끝점을 동일시하지만 그 외에는 단사이다. 따라서 $A$는 원과 동형이므로, 그 기본군은 무한 순환군이다. 실제로, 경로

$$\gamma (t)=(\cos (2\pi t/n),\sin (2\pi t/n))$$

가 $S^1$에서 $p$에서 $r(p)$로 가는 경로일 때, $\alpha =h\circ \gamma$는 ${\pi }_1(A,a)$의 생성원을 나타낸다.

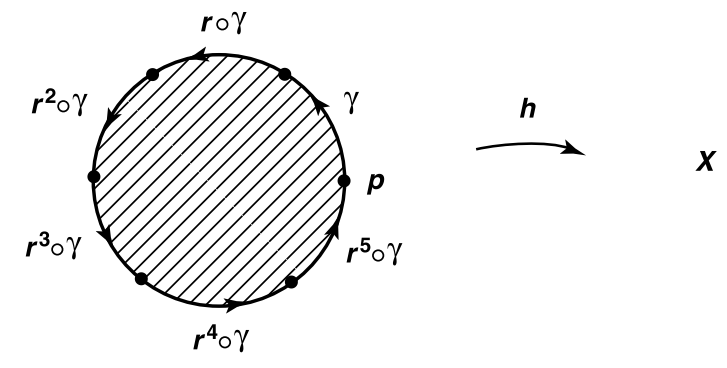
이제 고리

$$f=\gamma \ast (r\circ \gamma )\ast (r^2\circ \gamma )\ast \cdots \ast (r^{n-1}\circ \gamma )$$

는 ${\pi }_1(S^1,p)$를 생성한다. 모든 $x$와 $m$에 대해 $h(r^m(x))=h(x)$이므로, 고리 $h\circ f$는 n-겹 곱 $\alpha \ast (\alpha \ast (\cdots \ast \alpha ))$와 같다. 정리는 이로부터 따라온다.