70. The Seifert-van Kampen Theorem

§70 자이페르트-판 캄펀 정리 (The Seifert-van Kampen Theorem)

이제 우리는 두 개의 열린 부분집합 $U$와 $V$의 합으로 쓰여지고 경로 연결된 교집합을 가지는 공간 $X$의 기본군을 결정하는 문제로 돌아간다. 59. The Fundamental Group of Sⁿ에서 우리는 $x_0\in U\cap V$일 때, 포함사상에 의해 유도된 두 군 ${\pi }_1(U,x_0)$와 ${\pi }_1(V,x_0)$의 상(image)이 ${\pi }_1(X,x_0)$를 생성함을 보였다. 이 절에서는 ${\pi }_1(X,x_0)$가 사실상 이 두 군과 군 ${\pi }_1(U\cap V,x_0)$, 그리고 포함사상에 의해 유도된 여러 준동형사상들에 의해 완전히 결정됨을 보인다. 이것은 기본군에 대한 기본적인 결과이다. 이를 통해 우리는 콤팩트 2-다양체를 포함한 여러 공간의 기본군을 계산할 수 있게 될 것이다.

정리 70.1 (자이페르트-판 캄펀 정리)

$X=U\cup V$라 하자. 여기서 $U$와 $V$는 $X$에서 열린 집합이다. $U,V,U\cap V$는 경로 연결되어 있다고 가정하고, $x_0\in U\cap V$라 하자. $H$를 군이라 하고,

$${\varphi }_1:{\pi }_1(U,x_0)\to H\text{and}{\varphi }_2:{\pi }_1(V,x_0)\to H$$

를 준동형사상(homomorphism)이라고 하자. $i_1,i_2,j_1,j_2$를 다음 도표에 표시된, 각각 포함사상에 의해 유도된 준동형사상이라고 하자.

\usepackage{tikz-cd}
 
\begin{document}
 
\Large{
\begin{tikzcd}
& \pi_{1}(U,x_{0}) \arrow[d,"j_{1}"'] \arrow[dr,"\phi_{1}"] & \\
\pi_{1}(U\cap V,x_{0})
  \arrow[ur,"i_{1}"]
  \arrow[dr,"i_{2}"']
  \arrow[r] & \pi_{1}(X,x_{0})
  \arrow[r,dashed,"\Phi"] & H \\
& \pi_{1}(V,x_{0}) \arrow[u,"j_{2}"] \arrow[ur,"\phi_{2}"'] &
\end{tikzcd}
}
 
\end{document}

만약 ${\varphi }_1\circ i_1={\varphi }_2\circ i_2$이면, $\Phi \circ j_1={\varphi }_1$이고 $\Phi \circ j_2={\varphi }_2$를 만족하는 유일한 준동형사상 $\Phi :{\pi }_1(X,x_0)\to H$가 존재한다.

이 정리는 만약 ${\varphi }_1$과 ${\varphi }_2$가 ”$U\cap V$ 위에서 양립 가능한” 임의의 준동형사상이라면, 그들은 ${\pi }_1(X,x_0)$에서 $H$로 가는 준동형사상을 유도한다는 것을 말한다.

증명

유일성 은 쉽다. 정리 59.1에 따르면 ${\pi }_1(X,x_0)$는 $j_1$과 $j_2$의 상에 의해 생성된다. 생성원 $j_1(g_1)$에 대한 $\Phi$의 값은 ${\varphi }_1(g_1)$과 같아야 하고, $j_2(g_2)$에 대한 값은 ${\varphi }_2(g_2)$와 같아야 한다. 따라서 $\Phi$는 ${\varphi }_1$과 ${\varphi }_2$에 의해 완전히 결정된다.

존재성을 보이는 것은 다른 문제다!

편의상 다음 표기법을 도입한다: $X$ 안의 경로 $f$가 주어졌을 때, 우리는 $X$ 안에서 그것의 경로 동치류를 $[f]$로 나타낼 것이다. 만약 $f$가 $U$ 안에 있다면, $[f{]}_U$는 $U$ 안에서 그것의 경로 동치류를 나타내는 데 사용될 것이다. 표기법 $[f{]}_V$와 $[f{]}_{U\cap V}$도 비슷하게 정의된다.

1단계. 우리는 $U$ 또는 $V$에 있는 $x_0$를 시작점으로 하는 각 루프 $f$에 군 $H$의 원소를 할당하는 집합 사상 $\rho$를 정의하는 것으로 시작한다. 우리는 다음과 같이 정의한다.

$$\rho (f)=\{\begin{array}{ll}{\varphi }_1([f{]}_U)& \text{if }f\text{ lies in }U,\\ {\varphi }_2([f{]}_V)& \text{if }f\text{ lies in }V.\end{array}$$

$\rho$는 잘 정의된다. 왜냐하면 만약 $f$가 $U$와 $V$ 양쪽에 있다면,

$${\varphi }_1([f{]}_U)={\varphi }_1{i}_1([f{]}_{U\cap V})\text{and}{\varphi }_2([f{]}_V)={\varphi }_2{i}_2([f{]}_{U\cap V})$$

이며, 이 두 $H$의 원소는 가정에 의해 같기 때문이다. 집합 사상 $\rho$는 다음 조건들을 만족한다:

(1) $[f{]}_U=[g{]}_U$이거나 $[f{]}_V=[g{]}_V$이면, $\rho (f)=\rho (g)$이다. (2) $f$와 $g$가 둘 다 $U$에 있거나 둘 다 $V$에 있으면, $\rho (f\ast g)=\rho (f)\cdot \rho (g)$이다.

첫 번째는 정의에 의해 성립하고, 두 번째는 ${\varphi }_1$과 ${\varphi }_2$가 준동형사상이기 때문에 성립한다.

2단계. 이제 우리는 $\rho$를 $U$ 또는 $V$에 있는 경로 $f$에 $H$의 원소를 할당하는 집합 사상 $\sigma$로 확장하여, 사상 $\sigma$가 1단계의 조건 (1)을 만족하고, $f\ast g$가 정의될 때 (2)를 만족하도록 한다. 먼저, $X$의 각 점 $x$에 대해, $x_0$에서 $x$로 가는 경로 ${\alpha }_x$를 다음과 같이 선택한다: $x=x_0$이면, ${\alpha }_x$는 $x_0$에서의 상수 경로로 한다. $x\in U\cap V$이면, ${\alpha }_x$는 $U\cap V$ 안의 경로로 한다. 그리고 $x$가 $U$ 또는 $V$에 있지만 $U\cap V$에 있지 않으면, ${\alpha }_x$는 각각 $U$ 또는 $V$ 안의 경로로 한다. 그런 다음, $U$ 또는 $V$ 안의 임의의 경로 $f$에 대해, $U$ 또는 $V$ 안에서 $x_0$를 시작점으로 하는 루프 $L(f)$를 다음 방정식으로 정의한다.

$$L(f)={\alpha }_x\ast (f\ast {\bar{\alpha }}_y)$$

여기서 $x$는 $f$의 시작점이고 $y$는 끝점이다. 마지막으로,

$$\sigma (f)=\rho (L(f))$$

로 정의한다.

먼저, $\sigma$가 $\rho$의 확장임을 보인다. 만약 $f$가 $U$ 또는 $V$에 있는 $x_0$를 시작점으로 하는 루프라면, ${\alpha }_{x_0}$가 $x_0$에서의 상수 경로이므로

$$L(f)=e_{x_0}\ast (f\ast e_{x_0})$$

이다. 그러면 $L(f)$는 $U$ 또는 $V$에서 $f$와 경로 동치이므로, $\rho$에 대한 조건 (1)에 의해 $\rho (L(f))=\rho (f)$이다. 따라서 $\sigma (f)=\rho (f)$이다. 조건 (1)을 확인하기 위해, $f$와 $g$가 $U$ 또는 $V$에서 경로 동치인 경로라고 하자. 그러면 루프 $L(f)$와 $L(g)$ 또한 $U$ 또는 $V$에서 경로 동치이므로, $\rho$에 대한 조건 (1)이 적용된다. (2)를 확인하기 위해, $f(1)=g(0)$인 $U$ 또는 $V$ 안의 임의의 경로 $f$와 $g$를 보자. 우리는

$$L(f)\ast L(g)=({\alpha }_x\ast (f\ast {\bar{\alpha }}_y))\ast ({\alpha }_y\ast (g\ast {\bar{\alpha }}_z))$$

를 가진다. 적절한 점 $x,y,z$에 대해, 이 루프는 $U$ 또는 $V$에서 $L(f\ast g)$와 경로 동치이다. 그러면

$$\rho (L(f\ast g))=\rho (L(f)\ast L(g))=\rho (L(f))\cdot \rho (L(g))$$

가 $\rho$에 대한 조건 (1)과 (2)에 의해 성립한다. 따라서 $\sigma (f\ast g)=\sigma (f)\cdot \sigma (g)$이다.

3단계. 마지막으로, 우리는 $\sigma$를 $X$의 임의의 경로 $f$에 $H$의 원소를 할당하는 집합 사상 $\tau$로 확장한다. 이것은 다음 조건들을 만족할 것이다:

(1) $[f]=[g]$이면, $\tau (f)=\tau (g)$이다. (2) $f\ast g$가 정의되면, $\tau (f\ast g)=\tau (f)\cdot \tau (g)$이다.

$f$가 주어졌을 때, $f$가 각 부분구간 $[s_{i-1},s_i]$를 $U$ 또는 $V$로 보내는 $[0,1]$의 분할 $s_0<\cdots <s_n$을 선택하자. $f_i$를 $[0,1]$에서 $[s_{i-1},s_i]$로의 양의 선형 사상을 따른 후 $f$를 적용한 경로라고 하자. 그러면 $f_i$는 $U$ 또는 $V$ 안의 경로이고,

$$[f]=[f_1]\ast \cdots \ast [f_n]$$

이다. 만약 $\tau$가 $\sigma$의 확장이고 (1)과 (2)를 만족한다면, 우리는

$$\tau (f)=\sigma (f_1)\cdot \sigma (f_2)\cdots \sigma (f_n)(!)$$

를 가져야 한다. 그래서 우리는 이 방정식을 $\tau$의 정의로 사용할 것이다.

이 정의가 분할의 선택에 독립적임을 보인다. 단일 추가 점 $p$를 분할에 추가할 때 $\tau (f)$의 값이 변하지 않음을 보이는 것으로 충분하다. $s_{i-1}<p<s_i$인 인덱스 $i$가 있다고 하자. 이 새로운 분할을 사용하여 $\tau (f)$를 계산하면, 공식 (!)에서 유일한 변화는 $\sigma (f_i)$ 인자가 사라지고 $\sigma (f_i^{\prime })\cdot \sigma (f_i^{\prime \prime })$ 곱으로 대체되는 것이다. 여기서 $f_i^{\prime }$와 $f_i^{\prime \prime }$는 각각 $[0,1]$에서 $[s_{i-1},p]$와 $[p,s_i]$로의 양의 선형 사상을 따른 후 $f$를 적용한 것과 같다.

그러나 $f_i$는 $U$ 또는 $V$에서 $f_i^{\prime }\ast f_i^{\prime \prime }$와 경로 동치이므로, $\sigma$에 대한 조건 (1)과 (2)에 의해 $\sigma (f_i)=\sigma (f_i^{\prime })\cdot \sigma (f_i^{\prime \prime })$이다. 따라서 $\tau$는 잘 정의된다.

$\tau$가 $\sigma$의 확장임이 따라 나온다. 왜냐하면 만약 $f$가 이미 $U$ 또는 $V$에 있다면, 우리는 $[0,1]$의 자명한 분할을 사용하여 $\tau (f)$를 정의할 수 있고, 그러면 정의에 의해 $\tau (f)=\sigma (f)$이다.

4단계. 집합 사상 $\tau$에 대한 조건 (1)을 증명한다. 이 부분의 증명은 약간의 주의를 요한다. 우리는 먼저 특별한 경우에 이 조건을 확인한다. $f$와 $g$가 $X$에서 $x$에서 $y$로 가는 경로라고 하고, $F$가 그들 사이의 경로 동치라고 하자. $[0,1]$의 분할 $s_0,\dots ,s_n$이 존재하여 $F$가 각 사각형 $R_i=[s_{i-1},s_i]\times I$를 $U$ 또는 $V$로 보낸다는 추가 가정을 하자. 이 경우 $\tau (f)=\tau (g)$임을 보인다.

$i$가 주어졌을 때, $[0,1]$에서 $[s_{i-1},s_i]$로의 양의 선형 사상을 따른 후 $f$ 또는 $g$를 적용한 것을 각각 $f_i$와 $g_i$라고 하자. 사각형 $R_i$에 대한 $F$의 제한은 $U$ 또는 $V$에서 일어나는 $f_i$와 $g_i$ 사이의 동치를 제공하지만, 경로의 끝점이 동치 동안 움직일 수 있으므로 경로 동치는 아니다. 이 동치 동안 이 끝점들이 그리는 경로를 고려하자. ${\beta }_i(t)=F(s_i,t)$로 경로 ${\beta }_i$를 정의하자. 그러면 ${\beta }_i$는 $X$에서 $f(s_i)$에서 $g(s_i)$로 가는 경로이다. 경로 ${\beta }_0$와 ${\beta }_n$은 각각 $x$와 $y$에서의 상수 경로이다. 각 $i$에 대해,

$$f_i\ast {\beta }_i{\sim }_p{\beta }_{i-1}\ast g_i$$

이며, 경로 동치는 $U$ 또는 $V$에서 일어남을 보인다.

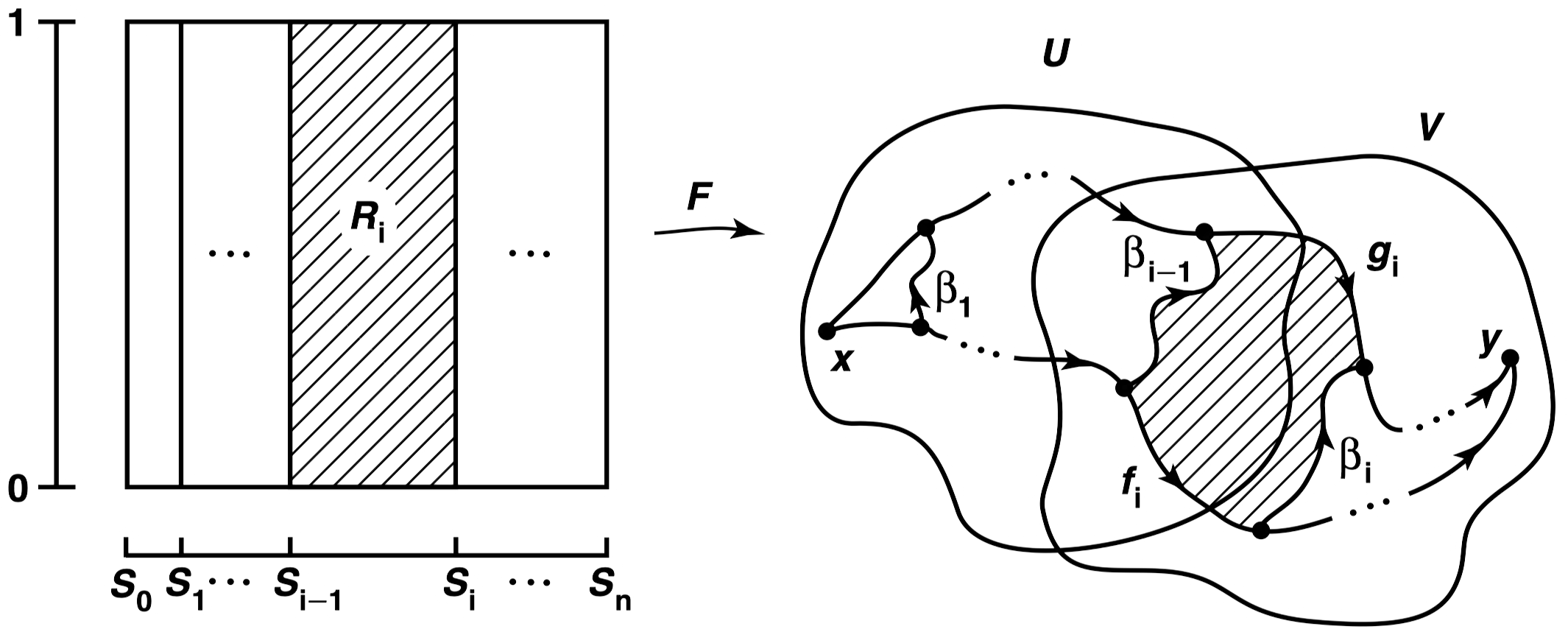
사각형 $R_i$에서, $s_{i-1}\times 0$에서 $s_i\times 0$을 거쳐 $s_i\times 1$로 가는 깨진 선 경로를 따라가면, 맵 $F$를 적용하면 경로 $f_i\ast {\beta }_i$를 얻는다. 비슷하게, $R_i$의 왼쪽과 위쪽 가장자리를 따라가는 깨진 선 경로를 따라가고 $F$를 적용하면 경로 ${\beta }_{i-1}\ast g_i$를 얻는다. $R_i$가 볼록하므로, 이 두 깨진 선 경로 사이에 $R_i$ 안의 경로 동치가 있다. $F$를 적용하면, $U$ 또는 $V$에서 일어나는 $f_i\ast {\beta }_i$와 ${\beta }_{i-1}\ast g_i$ 사이의 경로 동치를 얻는다.

$\sigma$에 대한 조건 (1)과 (2)로부터

$$\sigma (f_i)\cdot \sigma ({\beta }_i)=\sigma ({\beta }_{i-1})\cdot \sigma (g_i)$$

이므로,

$$\sigma (f_i)=\sigma ({\beta }_{i-1})\cdot \sigma (g_i)\cdot \sigma ({\beta }_i{)}^{-1}(\ast \ast )$$

이다. ${\beta }_0$와 ${\beta }_n$이 상수 경로이므로 $\sigma ({\beta }_0)=\sigma ({\beta }_n)=1$임이 비슷하게 따라 나온다. (왜냐하면 ${\beta }_0\ast {\beta }_0={\beta }_0$은 $\sigma ({\beta }_0)\cdot \sigma ({\beta }_0)=\sigma ({\beta }_0)$를 의미하기 때문이다.)

이제 다음과 같이 계산한다:

$$\tau (f)=\sigma (f_1)\cdot \sigma (f_2)\cdots \sigma (f_n)$$

이 방정식에 $(\ast \ast )$를 대입하고 단순화하면, 다음 방정식을 얻는다.

$$\tau (f)=\sigma (g_1)\cdot \sigma (g_2)\cdots \sigma (g_n)=\tau (g)$$

따라서, 우리는 특별한 경우에 조건 (1)을 증명했다.

이제 일반적인 경우에 조건 (1)을 증명한다. $f$와 $g$ 및 그들 사이의 경로 동치 $F$가 주어졌을 때, $[0,1]$의 분할 $s_0,\dots ,s_n$과 $t_0,\dots ,t_m$을 선택하여 $F$가 각 부분사각형 $[s_{i-1},s_i]\times [t_{j-1},t_j]$를 $U$ 또는 $V$로 보내도록 한다. $f_j(s)=F(s,t_j)$로 경로 $f_j$를 정의하자. 그러면 $f_0=f$이고 $f_m=g$이다. 경로 쌍 $f_{j-1}$과 $f_j$는 우리의 특별한 경우의 요구 사항을 만족하므로, 각 $j$에 대해 $\tau (f_{j-1})=\tau (f_j)$이다. 따라서 $\tau (f)=\tau (g)$이다.

5단계. 이제 집합 사상 $\tau$에 대한 조건 (2)를 증명한다. $X$ 안의 경로 $f\ast g$가 주어졌을 때, $f\ast g$가 각 부분구간을 $U$ 또는 $V$로 보내는 $[0,1]$의 분할 $s_0<\cdots <s_n$을 선택하자. 여기서 점 $1/2$을 분할 점으로 포함한다. $s_k=1/2$인 인덱스 $k$가 있다고 하자.

$i=1,\dots ,k$에 대해, $[0,1]$에서 $[s_{i-1},s_i]$로의 양의 선형 사상을 따른 후 $f\ast g$를 적용한 것은, $[0,1]$에서 $[2s_{i-1},2s_i]$로의 양의 선형 사상을 따른 후 $f$를 적용한 것과 같다. 이 맵을 $f_i$라고 하자. 비슷하게, $i=k+1,\dots ,n$에 대해, $[0,1]$에서 $[s_{i-1},s_i]$로의 양의 선형 사상을 따른 후 $f\ast g$를 적용한 것은, $[0,1]$에서 $[2s_{i-1}-1,2s_i-1]$로의 양의 선형 사상을 따른 후 $g$를 적용한 것과 같다. 이 맵을 $g_{i-k}$라고 하자. 경로 $f\ast g$의 정의역에 대한 분할 $s_0,\dots ,s_n$을 사용하면,

$$\tau (f\ast g)=\sigma (f_1)\cdots \sigma (f_k)\cdot \sigma (g_1)\cdots \sigma (g_{n-k})$$

이다. 경로 $f$에 대한 분할 $2s_0,\dots ,2s_k$를 사용하면,

$$\tau (f)=\sigma (f_1)\cdots \sigma (f_k)$$

이다. 그리고 경로 $g$에 대한 분할 $2s_k-1,\dots ,2s_n-1$을 사용하면,

$$\tau (g)=\sigma (g_1)\cdots \sigma (g_{n-k})$$

이다. 따라서 (2)는 자명하게 성립한다.

6단계. 정리는 이제 따라 나온다. $X$ 안에서 $x_0$를 시작점으로 하는 각 루프 $f$에 대해, 우리는 $\Phi ([f])=\tau (f)$로 정의한다. 조건 (1)과 (2)는 $\Phi$가 잘 정의된 준동형사상임을 보여준다. $\Phi \circ j_1={\varphi }_1$임을 보이자. 만약 $f$가 $U$ 안의 루프라면,

$$\Phi (j_1([f{]}_U))=\Phi ([f])=\tau (f)=\rho (f)={\varphi }_1([f{]}_U)$$

이다. $\Phi \circ j_2={\varphi }_2$라는 증명은 비슷하다.

이전 정리는 자이페르트-판 캄펀 정리의 현대적 공식이다. 이제 우리는 두 군의 자유 곱을 포함하는 고전적인 버전으로 넘어간다. $G$가 외부 자유 곱 $G=G_1\ast G_2$일 때, 우리는 표기의 단순화를 위해 종종 $G_1$과 $G_2$를 마치 $G$의 부분군인 것처럼 취급한다는 것을 상기하자.

정리 70.2 (자이페르트-판 캄펀 정리, 고전적 버전)

이전 정리의 가정을 따르자.

$$j:{\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)\to {\pi }_1(X,x_0)$$

를 포함사상에 의해 유도된 준동형사상 $j_1$과 $j_2$를 확장하는 자유 곱의 준동형사상이라고 하자. 그러면 $j$는 전사(surjective)이고, 그것의 핵(kernel)은 $g\in {\pi }_1(U\cap V,x_0)$에 대해

$$(i_1(g){)}^{-1}(i_2(g))$$

형태의 단어들로 표현되는 모든 원소들을 포함하는 자유 곱의 최소 정규 부분군(least normal subgroup) $N$이다.

달리 말하면, $j$의 핵은 $i_1(g{)}^{-1}{i}_2(g)$ 형태의 자유 곱의 모든 원소들과 그들의 켤레(conjugate)들에 의해 생성된다.

증명

${\pi }_1(X,x_0)$가 $j_1$과 $j_2$의 상에 의해 생성된다는 사실은 $j$가 전사임을 의미한다. $N\subset \text{ker }j$임을 보인다. $\text{ker }j$가 정규이므로, 각 $g\in {\pi }_1(U\cap V,x_0)$에 대해 $i_1(g{)}^{-1}{i}_2(g)$가 $\text{ker }j$에 속함을 보이는 것으로 충분하다. $i:U\cap V\to X$가 포함사상이라면,

$$j{i}_1(g)=j_1{i}_1(g)=i_{\ast }(g)=j_2{i}_2(g)=j{i}_2(g)$$

이다. 그러면 $i_1(g{)}^{-1}{i}_2(g)$는 $j$의 핵에 속한다. $j$가 전사 준동형사상

$$k:{\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)/N\to {\pi }_1(X,x_0)$$

를 유도함이 따라 나온다.

$k$가 단사(injective)임을 보여 $N$이 $\text{ker }j$와 같음을 보인다. $k$가 좌역원(left inverse)을 가짐을 보이는 것으로 충분하다.

$H$를 군 ${\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)/N$이라고 하자. ${\varphi }_1:{\pi }_1(U,x_0)\to H$를 ${\pi }_1(U,x_0)$를 자유 곱에 포함시킨 후, 그 자유 곱을 몫군 $N$으로 사영하는 것으로 하자. ${\varphi }_2:{\pi }_1(V,x_0)\to H$도 비슷하게 정의하자. 다음 도표를 고려하자.

\usepackage{tikz-cd}
 
\begin{document}
 
\Large{
\begin{tikzcd}
& \pi_{1}(U,x_{0}) \arrow[d,"j_{1}"'] \arrow[dr,"\phi_{1}"] & \\
\pi_{1}(U \cap V,x_{0})
  \arrow[ur,"i_{1}"]
  \arrow[r,"i_{*}"]
  \arrow[dr,"i_{2}"']
& \pi_{1}(X,x_{0})
    \arrow[r, dotted, shift right=0.4ex, "\Phi"'] 
& H
	\arrow[l, shift right=0.4ex, "k" above] \\
& \pi_{1}(V,x_{0}) \arrow[u,"j_{2}"] \arrow[ur,"\phi_{2}"'] &
\end{tikzcd}
}
\end{document}

${\varphi }_1\circ i_1={\varphi }_2\circ i_2$임을 쉽게 알 수 있다. 왜냐하면 $g\in {\pi }_1(U\cap V,x_0)$이면, ${\varphi }_1(i_1(g))$는 $H$에서 $i_1(g)N$ 잉여류이고, ${\varphi }_2(i_2(g))$는 $i_2(g)N$ 잉여류이기 때문이다. $i_1(g{)}^{-1}{i}_2(g)\in N$이므로, 이 잉여류들은 같다.

정리 70.1로부터 $\Phi \circ j_1={\varphi }_1$이고 $\Phi \circ j_2={\varphi }_2$인 준동형사상 $\Phi :{\pi }_1(X,x_0)\to H$가 존재함이 따라 나온다. $\Phi$가 $k$의 좌역원임을 보인다. $\Phi \circ k$가 $H$의 임의의 생성원, 즉 $g$가 ${\pi }_1(U,x_0)$ 또는 ${\pi }_1(V,x_0)$에 있는 $gN$ 형태의 임의의 잉여류 위에서 항등처럼 작용함을 보이는 것으로 충분하다. 그러나 $g\in {\pi }_1(U,x_0)$이면,

$$k(gN)=j(g)=j_1(g)$$

이므로,

$$\Phi (k(gN))=\Phi (j_1(g))={\varphi }_1(g)=gN$$

이다. $g\in {\pi }_1(V,x_0)$일 경우에도 비슷한 말이 적용된다.

보조정리 70.3

자이페르트-판 캄펀 정리의 가정을 따르자. 만약 $U\cap V$가 단일 연결(simply connected)이라면, 동형사상

$$k:{\pi }_1(U,x_0)\ast {\pi }_1(V,x_0)\to {\pi }_1(X,x_0)$$

가 존재한다.

보조정리 70.4

자이페르트-판 캄펀 정리의 가정을 따르자. 만약 $V$가 단일 연결이라면, 동형사상

$$k:{\pi }_1(U,x_0)/N\to {\pi }_1(X,x_0)$$

가 존재한다. 여기서 $N$은 준동형사상

$$i_1:{\pi }_1(U\cap V,x_0)\to {\pi }_1(U,x_0)$$

의 상을 포함하는 ${\pi }_1(U,x_0)$의 최소 정규 부분군이다.

예제 1

$X$를 세타-공간(theta-space)이라고 하자. 그러면 $X$는 세 개의 호 $A,B,C$의 합으로 이루어진 하우스도르프 공간이며, 각 쌍은 정확히 그들의 끝점 $p$와 $q$에서만 교차한다. 우리는 이전에 $X$의 기본군이 아벨 군이 아님을 보였다. 이제 이 군이 사실상 두 개의 생성원을 가지는 자유 군임을 보인다. $A$의 내점 $a$와 $B$의 내점 $b$를 선택하자. $X$를 열린 집합 $U=X-a$와 $V=X-b$의 합으로 쓰자. 공간 $U\cap V=X-a-b$는 축약 가능(contractible)하므로 단일 연결이다. 더욱이, $U$는 $B\cup C$와 호모토피 동치이고 $V$는 $A\cup C$와 호모토피 동치이므로, $U$와 $V$는 무한 순환 기본군을 가진다. 따라서, $X$의 기본군은 두 개의 무한 순환군의 자유 곱이며, 즉 두 개의 생성원을 가지는 자유 군이다.