원뿔곡선과 주축정리

원뿔 곡선 (Conic Sections)

다음과 같은 이차 방정식을 고려하자.

$$a{x}^2+2bxy+c{y}^2+dx+ey+f=0\text{\hspace{1em}(1)}$$

특정 계수 값을 선택하면, 우리는 다양한 원뿔 곡선을 얻을 수 있다. 예를 들어, $a=c=1$, $b=d=e=0$, $f=-1$을 선택하면 원점 중심의 원 $x^2+y^2=1$을 얻게 된다. 나머지 원뿔 곡선(타원, 포물선, 쌍곡선)은 계수의 다른 선택을 통해 얻어진다.

만약 $b=0$이라면, $xy$ 항이 없으므로 완전제곱법을 이용하여 방정식을 쉽게 그래프로 나타낼 수 있다. 예를 들어, 방정식

$$x^2+2x+y^2+4y+2=0$$

는 완전제곱법을 이용하여 다음과 같이 변형될 수 있다.

$$(x+1{)}^2+(y+2{)}^2=3$$

이는 반지름이 $\sqrt{3}$이고 중심이 $(-1,-2)$인 원을 나타낸다. 좌표 변환

$$(x,y)\to (x^{\prime },y^{\prime }),x^{\prime }=x+1,y^{\prime }=y+2$$

을 고려하면 방정식은 단순한 형태인

$$(x^{\prime }{)}^2+(y^{\prime }{)}^2=3$$

로 변환된다. 이러한 변수 변환을 통해 $x$ 및 $y$ 항을 제거할 수 있다.

동반된 이차형식(associated quadratic form)

이제 우리는 $xy$ 항의 제거에 집중한다. 이를 위해, 다음과 같은 동반된 이차 형식(associated quadratic form)을 고려한다.

$$a{x}^2+2bxy+c{y}^2\text{\hspace{1em}(2)}$$

행렬을 다음과 같이 정의하면,

$$A=\left(\begin{array}{cc}a& b\\ b& c\end{array}\right),X=\left(\begin{array}{c}x\\ y\end{array}\right)$$

위 식은 다음과 같이 표현될 수 있다.

$$X^{t}AX=⟨AX,X⟩$$

예를 들어, 이차 형식 $3x^2+4xy+6y^2$는 행렬 표현으로 다음과 같이 나타낼 수 있다.

$$X^t\left(\begin{array}{cc}3& 2\\ 2& 6\end{array}\right)X$$

행렬 $A$가 대칭 행렬이라는 점이 중요한 역할을 한다. 대칭행렬은 실대각행렬과 직교동치(orthognally equivalent)이므로, 우리는 직교 행렬 $P$와 대각 행렬 $D$를 선택할 수 있으며, 이때 $D$의 대각 원소는 실수 고윳값 ${\lambda }_1,{\lambda }_2$이다. 즉,

$$P^{t}AP=D$$

이제 다음과 같이 새로운 좌표를 정의한다.

$$X^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$$

여기서,

$$X^{\prime }=P^{t}X$$

혹은 동등하게,

$$P{X}^{\prime }=X\Rightarrow P{P}^{t}X=X$$

이제,

$$X^{t}AX=(P{X}^{\prime }{)}^{t}A(P{X}^{\prime })=X^{\prime t}(P^{t}AP)X^{\prime }=X^{\prime t}D{X}^{\prime }={\lambda }_1(x^{\prime }{)}^2+{\lambda }_2(y^{\prime }{)}^2$$

따라서 좌표 변환 $(x,y)\to (x^{\prime },y^{\prime })$를 수행하면, 주어진 방정식에서 $xy$ 항을 제거할 수 있다.

추가적으로, $P$가 직교 행렬이므로,

$$\det (P)=\pm 1$$

만약 $\det (P)=-1$이라면, 우리는 $P$의 열 벡터를 바꾸어 행렬 $Q$를 얻을 수 있다. 행렬 $P$의 열 벡터는 $A$의 고유 벡터 정규 직교 기저(orthonormal basis of eigenvectors)를 이루므로, $Q$도 마찬가지다. 따라서,

$$Q^{t}AQ=\left(\begin{array}{cc}{\lambda }_2& 0\\ 0& {\lambda }_1\end{array}\right)$$

$\det (Q)=-\det (P)=1$임을 주목하자. 따라서, 만약 $\det (P)=-1$이라면, 우리는 $Q$를 새로운 $P$로 선택할 수 있다. 따라서 항상 $\det (P)=1$이 되도록 $P$를 선택할 수 있다. ($\det (P)=1$인 직교 행렬 $P$는 회전을 나타낸다.)

요약하면, 식 (2)에 있는 $xy$ 항은 $x$-축과 $y$-축을 새로운 축 $x^{\prime }$ 및 $y^{\prime }$로 회전시켜 제거할 수 있으며, 이는

$$X=P{X}^{\prime }$$

로 주어진다. 여기서 $P$는 직교 행렬이며, $\det (P)=1$이다. 또한, $(x^{\prime }{)}^2$과 $(y^{\prime }{)}^2$의 계수는 행렬

$$A=\left(\begin{array}{cc}a& b\\ b& c\end{array}\right)$$

의 고윳값들이다.

이 결과는 주축 정리 (principal axis theorem)의 재진술이다. 위의 논의는 $n$개의 변수를 가지는 이차 방정식으로 쉽게 확장될 수 있다. 예를 들어, $n=3$인 경우, 계수의 특수한 선택을 통해 이차 곡면(quadratic surfaces)을 얻을 수 있다. 즉, 타원형 원뿔(elliptic cone), 타원체(ellipsoid), 쌍곡 포물면(hyperbolic paraboloid) 등이 포함된다.

활용

다음과 같은 이차 방정식을 고려하자.

$$2x^2-4xy+5y^2-36=0$$

이 방정식에 대응하는 동반된 이차 형식(associated quadratic form)은

$$2x^2-4xy+5y^2$$

이다. 우리가 사용한 행렬 표기법을 적용하면,

$$A=\left(\begin{array}{cc}2& -2\\ -2& 5\end{array}\right)$$

이 된다. 이 행렬의 고윳값은 $1$과 $6$이며, 이에 대응하는 고유벡터(eigenvectors)는 다음과 같다.

$$\left(\begin{array}{c}2\\ 1\end{array}\right),\left(\begin{array}{c}-1\\ 2\end{array}\right)$$

두 고윳값은 서로 다르므로, 이 벡터들은 서로 직교(orthogonal)하다. 이에 대응하는 직교 정규 기저(orthonormal basis of eigenvectors)는 다음과 같다.

$$\beta =\left\{\left(\begin{array}{c}\frac{2}{\sqrt{5}}\\ \frac{1}{\sqrt{5}}\end{array}\right),\left(\begin{array}{c}\frac{-1}{\sqrt{5}}\\ \frac{2}{\sqrt{5}}\end{array}\right)\right\}$$

이러한 기저 벡터는 새로운 좌표축 $x^{\prime }$ 및 $y^{\prime }$을 결정하며, 이는 그림 6.4에서 볼 수 있다. 따라서 행렬 $P$를 다음과 같이 정의할 수 있다.

$$P=\left(\begin{array}{cc}\frac{2}{\sqrt{5}}& \frac{-1}{\sqrt{5}}\\ \frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}\end{array}\right)=\frac{1}{\sqrt{5}}\left(\begin{array}{cc}2& -1\\ 1& 2\end{array}\right)$$

그렇다면

$$P^{t}AP=\left(\begin{array}{cc}1& 0\\ 0& 6\end{array}\right)$$

이 된다.

좌표 변환 $X=P{X}^{\prime }$을 적용하면,

$$x=\frac{2}{\sqrt{5}}{x}^{\prime }-\frac{1}{\sqrt{5}}{y}^{\prime }$$ $$y=\frac{1}{\sqrt{5}}{x}^{\prime }+\frac{2}{\sqrt{5}}{y}^{\prime }$$

이 된다.

이를 이용하면 새로운 이차 형식은

$$(x^{\prime }{)}^2+6(y^{\prime }{)}^2$$

로 변환된다. 따라서 원래의 방정식

$$2x^2-4xy+5y^2=36$$

은 새로운 좌표계에서

$$(x^{\prime }{)}^2+6(y^{\prime }{)}^2=36$$

으로 나타낼 수 있다. 여기서 $x^{\prime }$-축과 $y^{\prime }$-축은 각각 $\beta$의 첫 번째 및 두 번째 고유벡터의 방향을 따른다. 이 방정식은 타원(ellipse)을 나타낸다는 것이 명백하다.

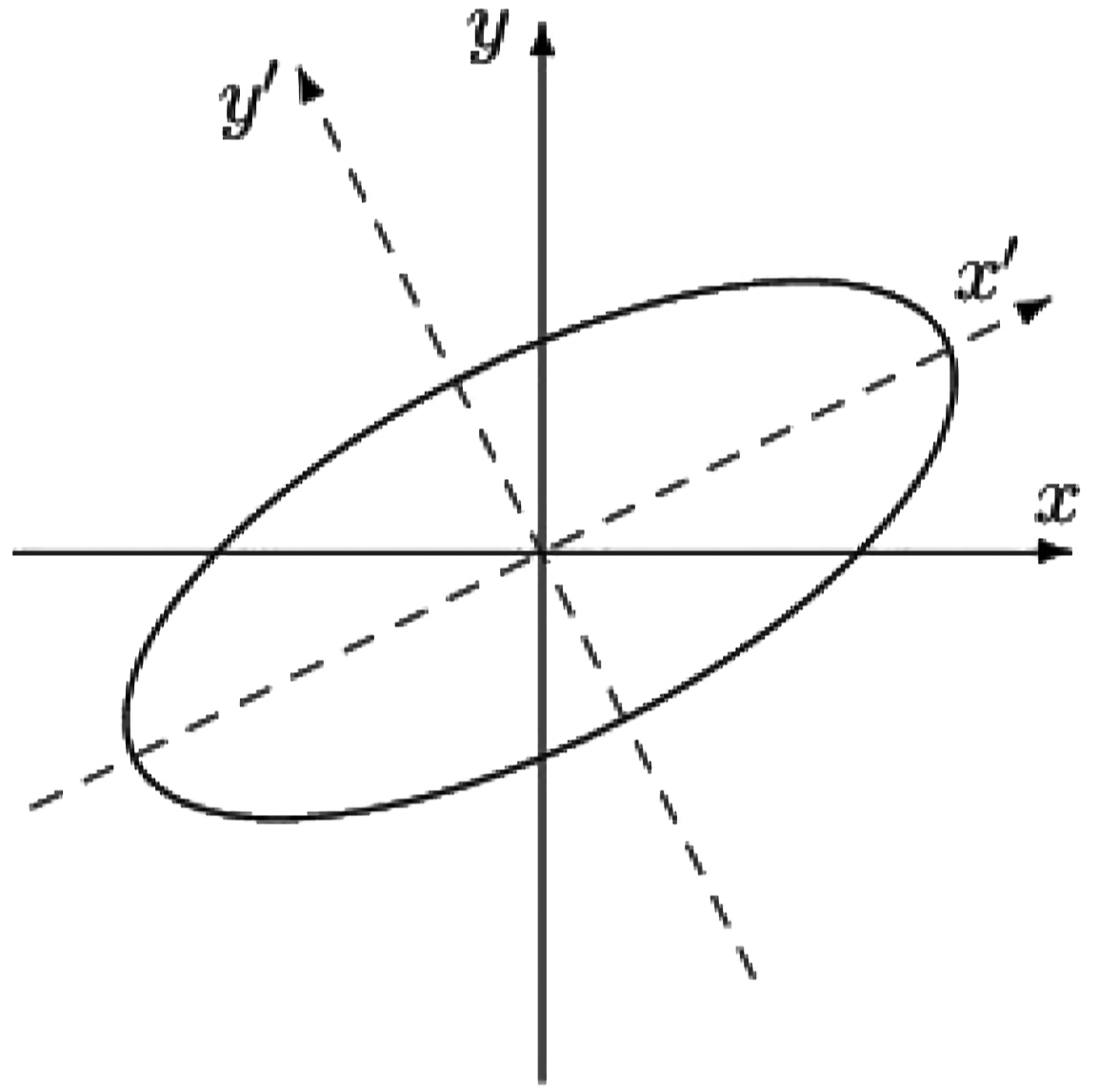
주어진 행렬 $P$는 다음과 같은 형태를 가진다.

$$\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$$

여기서

$$\theta ={\cos }^{-1}\left(\frac{2}{\sqrt{5}}\right)\approx 26.6^{\circ }$$

즉, $P$는 ${\mathbb{R}}^2$에서 각도 $\theta$만큼의 회전을 나타내는 행렬이다. 따라서 변수 변환 $X=P{X}^{\prime }$는 $x$-축과 $y$-축을 회전하여 수행할 수 있다.

그러나 $P$에는 또 다른 선택이 존재한다. 만약 행렬 $A$의 고윳값 $6$에 대응하는 고유벡터를 $(-1,2)$ 대신 $(1,-2)$로 선택하고, 고윳값들의 순서를 바꾼다면, 다음과 같은 행렬을 얻을 수 있다.

$$\left(\begin{array}{cc}\frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}\\ \frac{-2}{\sqrt{5}}& \frac{1}{\sqrt{5}}\end{array}\right)$$

이 행렬은 다음과 같은 각도 $\theta$를 갖는 회전 행렬을 나타낸다.

$$\theta ={\sin }^{-1}\left(\frac{-2}{\sqrt{5}}\right)\approx -63.4^{\circ }$$

이 경우, 결과적으로 동일한 타원이 생성되지만, $x^{\prime }$-축과 $y^{\prime }$-축의 이름이 서로 바뀐다.