이 절에서는 정칙이고 가향인 곡면 에 방향(orientation) 이 주어졌다고 가정한다.
가우스 사상 (Gauss Map)
방향이 주어진 곡면 에 대하여, 사상 는 의 각 점 에 단위 법선벡터 를 대응시킨다. 여기서 는 반지름이 1인 단위구면 이다.
이렇게 정의된 사상 을 곡면 의 가우스 사상(Gauss map)이라 한다.
가우스 사상 은 미분가능하다. 점 에서 의 미분 는 에서 로 가는 선형사상이다. 와 는 에서 평행한 평면들이므로, 동일한 벡터 공간으로 볼 수 있다. 따라서 는 위의 선형 연산자로 간주할 수 있다.
는 점 근방에서 법선벡터 이 어떻게 변하는지를 측정한다. 곡선에서 이 변화율이 곡률이라는 하나의 수로 주어졌다면, 곡면에서는 이 변화율이 선형사상으로 특징지어진다.
단위 법벡터장 의 미분
함수 , 즉 입력은 , 출력은 이다. 따라서 미분 는 다음과 같은 선형 변환이 된다.
즉, 도함수는 개의 성분 각각을 와 로 편미분한 행 열 행렬로 표현된다:
합성함수
에 대해, 체인 룰에 의해 다음과 같이 미분된다.
즉, 도함수 행렬()에 파라미터 변화율 벡터()를 곱해 3차원 벡터로서 의 변화율을 얻는다.
이는 를 따라가는 법벡터장의 변화율을 정확히 묘사한다.
제2 기본 형식 (The Second Fundamental Form)
가우스 사상의 미분 는 자기수반(self-adjoint) 선형사상이다.
가 선형사상이므로, 의 기저 에 대해 임을 보이면 충분하다. 이고 이므로, 우리는 임을 보이면 된다. 과 을 각각 와 에 대해 편미분하면 다음을 얻는다.
따라서 이다.
위에 정의된 이차 형식1
을 점 에서 곡면 의 제2 기본 형식(second fundamental form)이라 한다.
법곡률 (Normal Curvature)
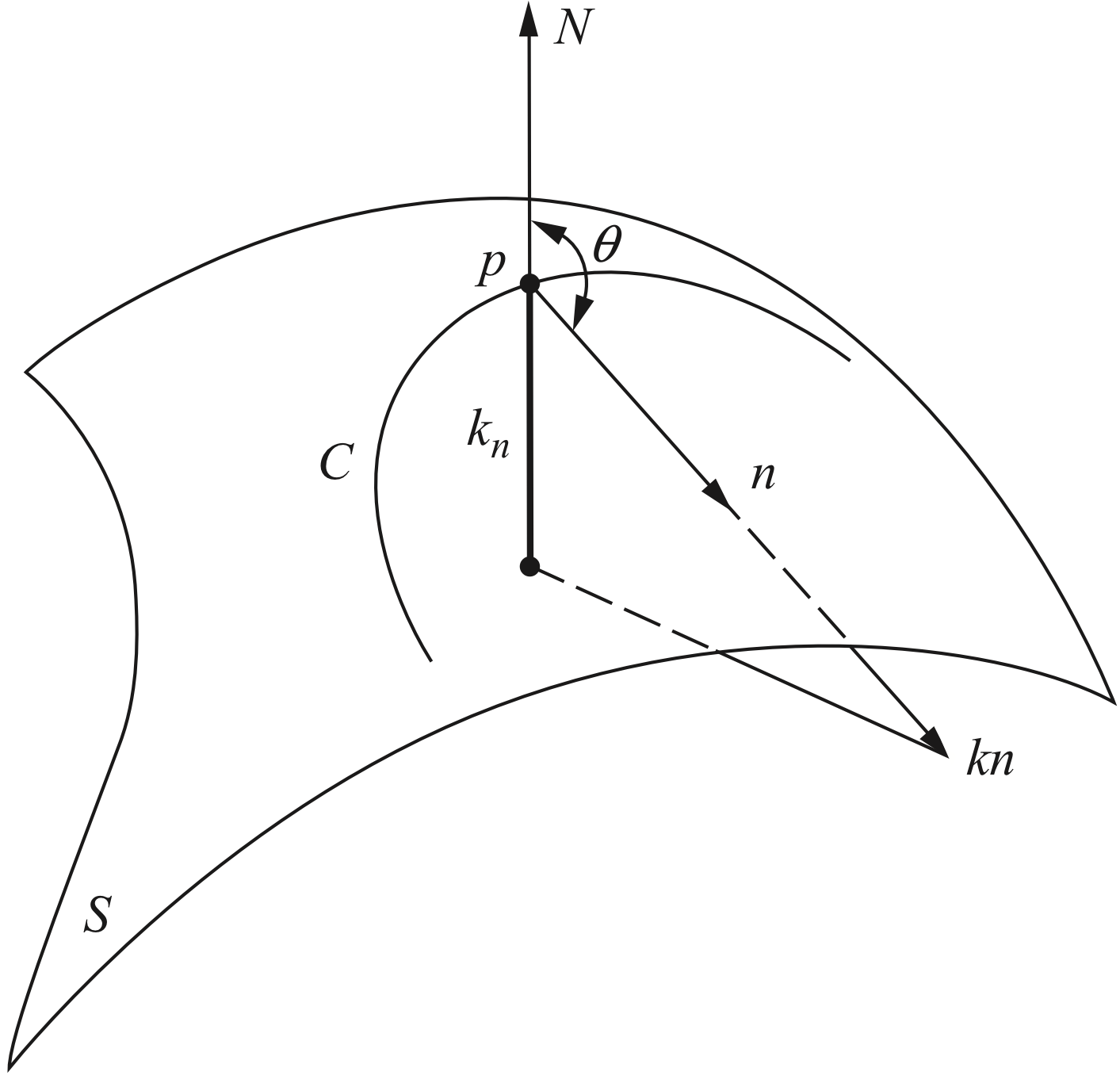
곡면 위의 정칙 곡선 가 점 를 지난다고 하자. 의 점 에서의 곡률을 라 하고, 의 법선벡터를 , 의 법선벡터를 이라 할 때, 이다. 이때 수 를 점 에서 곡선 의 법곡률(normal curvature)이라 한다.
법곡률 은 곡률벡터 을 곡면의 법선 방향으로 정사영한 것의 부호 있는 길이가 된다.
를 호의 길이로 갖는 곡선 가 를 만족할 때, 이므로 이고, 제2 기본 형식의 값은 다음과 같이 법곡률과 같다.
뫼니에 정리(Meusnier’s Theorem)
한 점 를 지나고 같은 접선을 갖는 곡면 위의 모든 곡선들은 그 점에서 같은 법곡률을 갖는다.
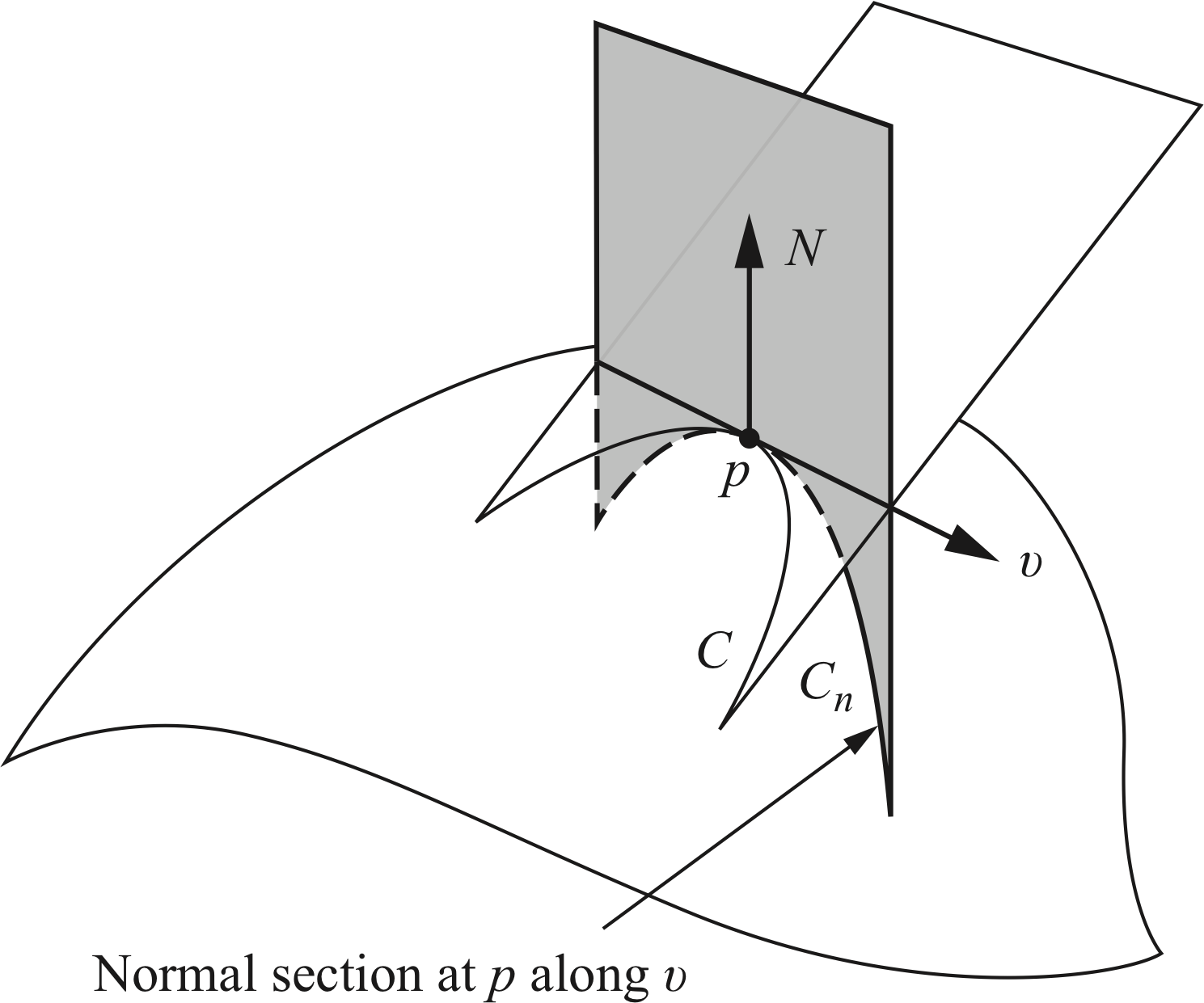
이 정리에 의해 한 점 에서 주어진 방향으로의 법곡률을 이야기할 수 있다. 단위벡터 가 주어졌을 때, 와 를 포함하는 평면과 곡면 의 교선을 점 에서 방향의 법절단면(normal section)이라 한다. 법절단면의 곡률은 그 방향의 법곡률의 절댓값과 같다.
주곡률과 주방향(Principal Curvatures and Principal Directions)
가 자기수반이므로, 에는 , 를 만족하는 정규직교기저 가 존재한다. 이때 과 는 제2 기본 형식 가 단위 원 위에서 갖는 최댓값과 최솟값, 즉 법곡률의 극값이다.
-
최대 법곡률 과 최소 법곡률 를 점 에서의 주곡률(principal curvatures)이라 하고, 이에 대응하는 고유벡터 의 방향을 주방향(principal directions)이라 한다.
-
곡면 위의 정칙 연결 곡선 의 모든 점 에서 의 접선이 주방향일 때, 를 의 곡률선(line of curvature)이라 한다.2
-
올랭드 로드리그(Olinde Rodrigues): 연결된 정칙 곡선 가 곡률선이 될 필요충분조건은 임의의 매개화 에 대해 를 만족하는 것이다. 여기서 이고, 는 미분가능한 함수이다. 이 경우, 는 방향의 주곡률이다.
-
오일러 공식 (Euler’s Formula): 주방향 과 각 를 이루는 단위벡터 방향의 법곡률 은 다음과 같다.
가우스 곡률과 평균 곡률 (Gaussian and Mean Curvatures)
점 에서 가우스 사상의 미분 에 대하여,
- 의 행렬식(determinant)을 점 에서 의 가우스 곡률(Gaussian curvature) 라 한다.
- 의 대각합(trace)의 배를 점 에서 의 평균 곡률(mean curvature) 라 한다.
주곡률 를 이용하여 다음과 같이 표현할 수 있다.
곡면 위의 한 점은 다음과 같이 분류된다.
- 점 에서 이면 를 배꼽점(umbilical point)이라 한다. 특히, 평탄점()은 배꼽점이다. 연결된 곡면 의 모든 점이 배꼽점이면, 는 평면의 일부이거나 구면의 일부이다.
점근 방향 (Asymptotic Directions)
점 에서 법곡률이 이 되는 의 방향을 점근 방향(asymptotic direction)이라 한다. 위의 정칙 연결 곡선 의 각 점 에서 의 접선 방향이 점근 방향일 때, 를 점근선(asymptotic curve)이라 한다.
- 타원점에서는 점근 방향이 존재하지 않는다.
듀팽의 지시곡선(Dupin Indicatrix)
점 에서의 듀팽 지시곡선은 을 만족하는 벡터 들의 집합이다. 를 주방향의 정규직교기저라 하고 라 하면, 지시곡선의 방정식은 다음과 같다.
- 타원점 (): 지시곡선은 타원이다.
- 쌍곡점 (): 지시곡선은 한 쌍의 공통 점근선을 갖는 두 쌍곡선이다. 이 점근선 방향이 바로 점근 방향이다. 따라서 쌍곡점에서는 정확히 두 개의 점근 방향이 존재한다.
- 포물점 (): 지시곡선은 한 쌍의 평행한 직선이다. 이 직선들의 공통 방향이 유일한 점근 방향이다.
켤레 (conjugate)
점 에서 영이 아닌 두 벡터 가 을 만족할 때,7 이 두 벡터는 켤레(conjugate)이라고 한다. 점 에서 두 방향 와 각각 평행한 영벡터가 아닌 두 벡터 가 켤레이면, 는 켤레 방향(conjugate directions)이라고 한다.
- 주방향은 항상 서로 켤레이다. 점근 방향은 자기 자신과 켤레이다. 배꼽점이 아닌 점에서, 두 방향 가 주방향 과 이루는 각을 각각 라 할 때, 두 방향이 켤레일 필요충분조건은 다음과 같다.