가로가 , 세로가 인 직사각형을 한 변의 길이가 (는 자연수)인 정사각형의 타일로 빈틈없이 채우려면 가로와 세로가 모두 의 배수이므로 는 과 의 공약수여야 한다. 이때, 과 의 최대공약수는 의 최대값이므로, 직사각형을 같은 크기의 정사각형으로 나누었을 때 얻을 수 있는 정사각형의 변의 길이의 최대값이다.
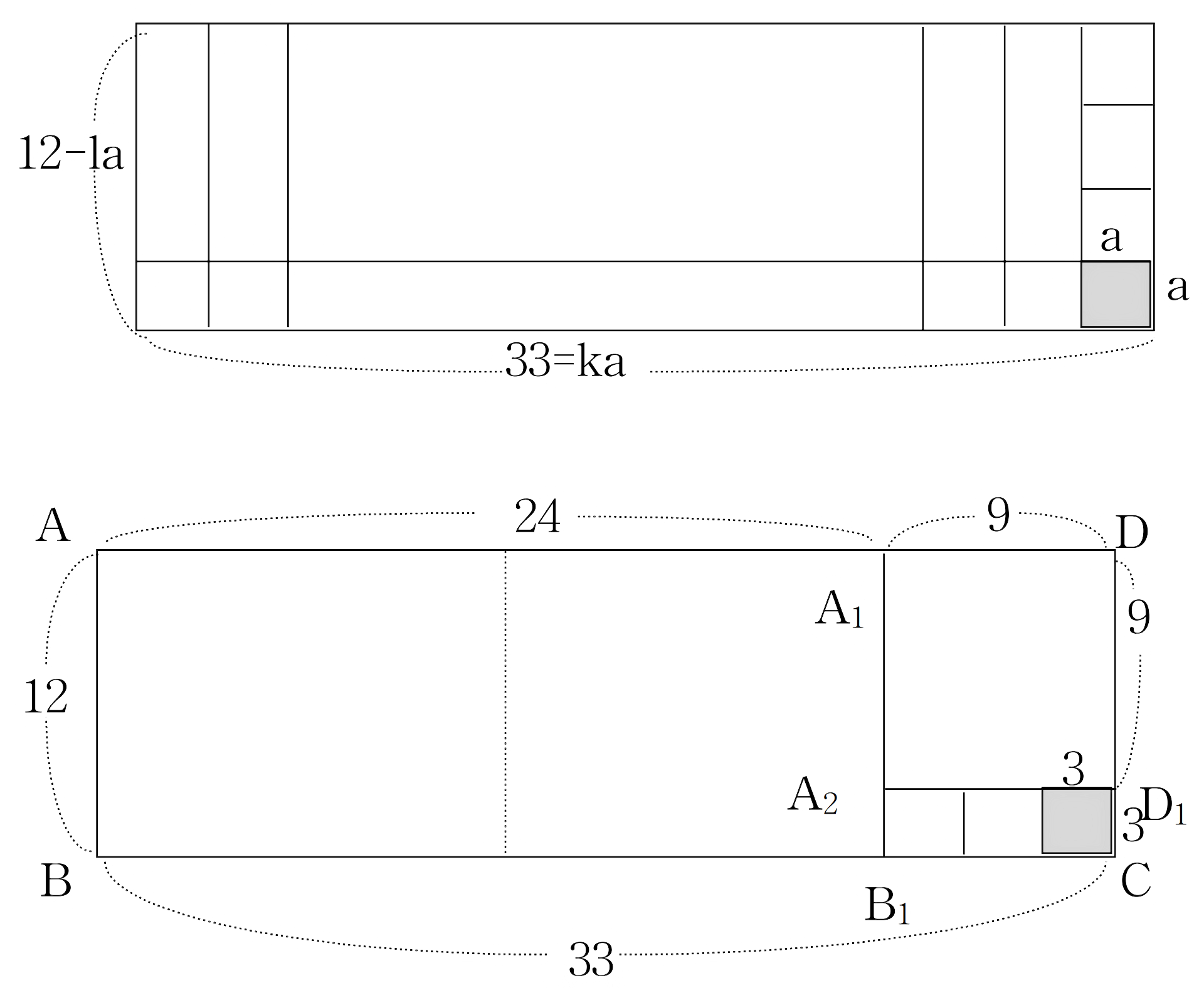
그림에서 을 로 나누면
이므로 □ 에 내접하는 정사각형의 최대 변의 길이는 보다 작으므로 나머지 부분인 가로 ( 을 로 나눈 나머지)와 세로 인 직사각형 에 내접하는 정사각형의 최대 변의 길이와 같다.
다시, 를 로 나누면
이므로 정사각형의 최대 변의 길이는 보다 작으며 나머지 부분인 세로가 (를 로 나눈 나머지), 가로가 인 직사각형 에 내접하는 최대 변의 길이와 같다.
그런데
이므로 □ 에 내접하는 정사각형의 최대 변의 길이는 이다. 즉, 과 의 최대공약수는 이다. 위의 과정을 정리하면 다음과 같다.
정리
증명
를 로 나누었을 때 몫을 , 나머지를 라 하면
이때, 의 최대공약수를 , 의 최대공약수를 이라 하자.
-
에서 이므로 는 의 약수이다. 는 의 공약수 이므로, 는 의 최대공약수인 의 약수이다.
-
이라 하면 이므로 는 의 약수이다. 는 의 공약수 이므로, 는 의 최대공약수인 의 약수이다.
1, 2에서 와 은 서로 약수이므로 이다. 즉, 의 최대공약수와 의 최대공약수는 서로 같다.
유클리드 호제법(Euclidean Algorithm)
일 때, 다음과 같이 나머지를 반복적으로 구한다.
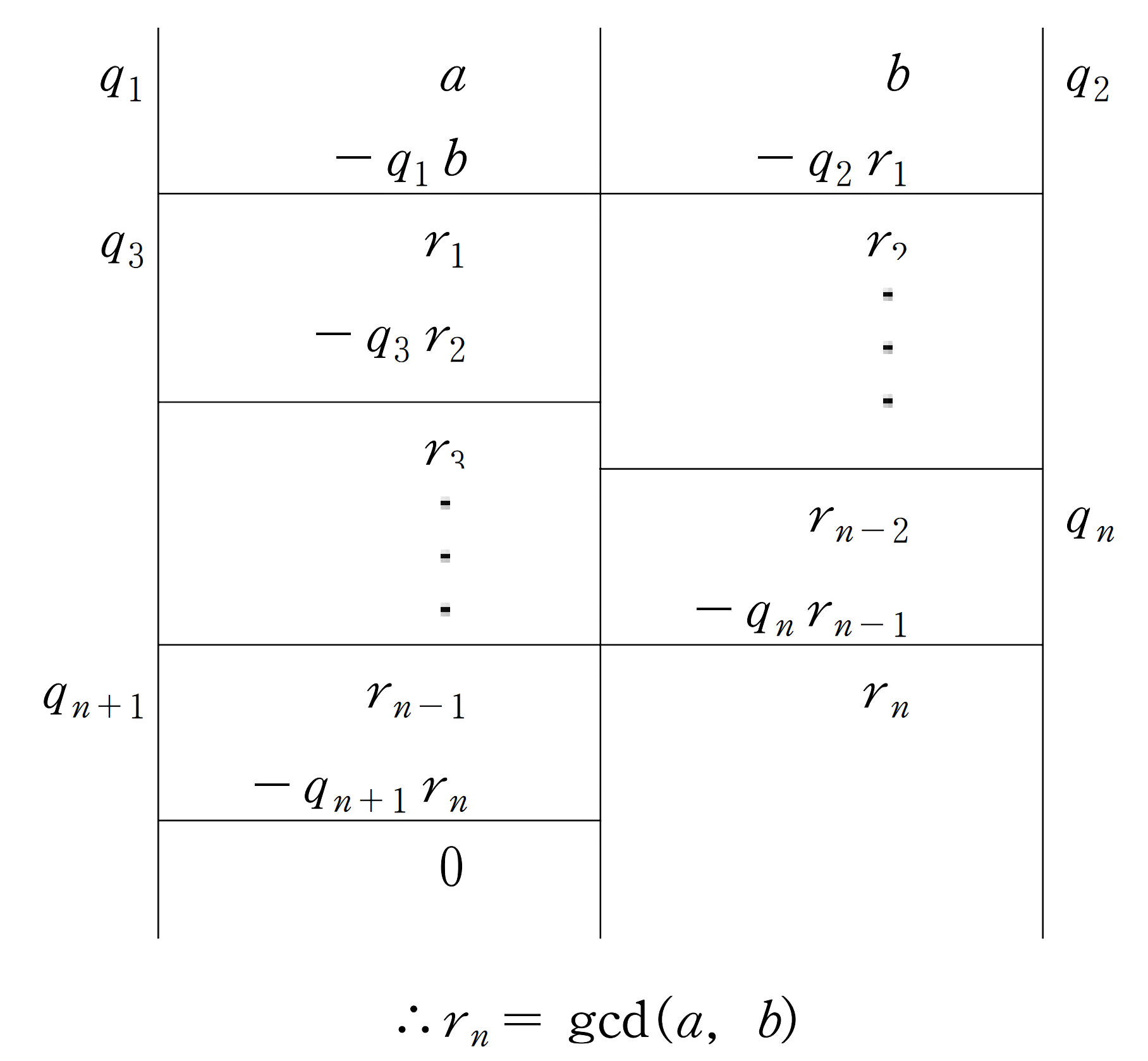
예시 1
두 자연수 , 의 최대공약수를 구하여라.
따라서 이다.
베주 항등식(Bézout’s identity)
유클리드 호제법을 이용하여 주어진 두 정수 의 최대공약수 를 구할 수 있을 뿐만 아니라 를 만족시키는 정수 쌍 도 얻을 수 있다. 그 방법은 다음과 같다.
에
를 대입하면
여기에
를 대입하면
다시 여기에
를 대입한다. 이와 같은 과정을 되풀이하면 를 만족시키는 정수 쌍 를 구할 수 있다.
예시 2
다음 식을 만족하는 정수 중 하나를 구하여라.
유클리드 호제법에 의해
이다. 이제 유클리드 호제법을 역추적하여 를 만족하는 정수 를 구하면
, 이다.
유클리드 호제법 표를 이용하면
이므로 , 이다.
서로소의 성질
정수 가 일 때, 와 가 서로소(relatively prime)이기 위한 필요충분조건은 다음과 같다.
증명
(⇐ 방향)
정수 가 존재하여 이면, 모든 의 공약수 는 를 나누어야 하므로 이다. 따라서 이므로
(⇒ 방향)
이라면, 유클리드 호제법을 통해 를 구하는 과정을 역추적하여
항상 의 꼴로 표현할 수 있다.
유일한가?
에 대해
을 만족하는 어떤 하나의 정수 해 가 존재한다고 하자. 그러면 이 방정식의 모든 해는 다음과 같이 일반해의 형태로 표현된다.
즉, 에 정수 값을 마음대로 넣으면 무한히 많은 쌍이 나온다.
예시 3
한 해는 이다.
하지만 이외에도
처럼 무수히 많은 정수해가 존재한다.
예제
-
를 구하시오.1
-
를 구하시오.2
-
를 구하시오.3
-
두 자연수 과 (이 개)의 최대 공약수를 구하시오.4
-
임의의 자연수 에 대하여 이 기약분수임을 증명하시오. 5
-
임의의 자연수 에 대하여 가 기약분수임을 증명하시오.6
-
를 만족하는 정수 를 하나만 구하여라. 7