The Urysohn Lemma

유리손 보조정리(Urysohn lemma)

정규 공간 $X$ 에서 서로소인 두 닫힌집합 $A, B$ 가 있다고 하자. 실직선 위의 닫힌구간 $[a, b]$ 에 대해, 모든 $x \in A$ 와 모든 $x \in B$ 에 대하여, 다음을 만족하는 연속함수

f : X ⟶ [a, b]

가 존재한다.

증명

구간이 $[a, b]$ 일 때의 일반적인 경우는 $[0, 1]$ 의 경우로부터 쉽게 따라오므로, $[0, 1]$ 인 경우만 증명하면 충분하다.

증명의 첫 번째 단계는, 정규성을 이용하여 $X$ 의 열린집합들로 이루어진 어떤 족 $U_{p}$ 를 구성하는 것이다. 이 집합들은 유리수들을 지표로 하여 구성되며, 이 열린집합들을 이용해 연속함수 $f$ 를 정의하게 된다.

Step 1.

구간 $[0, 1]$ 에 속하는 모든 유리수들의 집합을 $P$ 라 하자. 우리는 $P$ 의 각 원소 $p$ 에 대해, 열린집합 $U_{p} \subset X$ 를 다음 조건을 만족하도록 정의할 것이다.

p < q \Rightarrow \overline{U_{p}} \subset U_{q} .

이 조건을 만족하므로, $U_{p}$ 들의 족은 유리수들의 표준적인 순서와 같은 방식으로 포함관계에 따라 단순히 정렬된다.

$P$ 는 가산집합이므로, 우리는 유도(정확히는 재귀정의의 원리)를 통해 $U_{p}$ 들을 정의할 수 있다. $P$ 의 원소들을 어떤 순서로든 배열한 뒤, 편의를 위해 처음 두 항을 $1$ 과 $0$ 이라고 하자.

이제 다음과 같이 $U_{p}$ 들을 정의한다. 우선 $U_{1} = X - B$ 로 둔다. 다음으로, $A$ 는 닫힌집합이고 $U_{1}$ 은 열린집합이므로, 정규성에 따라 다음 조건을 만족하는 열린집합 $U_{0}$ 가 존재한다.

A \subset U_{0}, \overline{U_{0}} \subset U_{1} .

일반적으로, $P_{n}$ 을 앞의 순서에서 첫 $n$ 개의 유리수로 이루어진 집합이라 하자. 귀납가정에 따라, $P_{n}$ 에 속하는 모든 $p$ 에 대해 $U_{p}$ 가 정의되어 있으며, 아래 조건을 만족한다고 하자.

(*) p < q \Rightarrow \overline{U_{p}} \subset U_{q} .

이제 다음 유리수 $r$ 에 대해 $U_{r}$ 을 정의하고자 한다.

$P_{n + 1} = P_{n} \cup {r}$ 는 유한집합이며, 실수의 표준적인 순서에서 유도된 간단한 순서를 갖는다. 유한한 단순정렬집합에서는 (가장 작은 원소와 가장 큰 원소를 제외하고) 모든 원소가 정확히 하나의 바로 앞 원소와 하나의 바로 뒤 원소를 가진다(Theorem 10.1 참고). 이때 $0$ 은 가장 작은 원소이고, $1$ 은 가장 큰 원소이며, $r$ 은 둘 다 아닌 경우이므로, $r$ 은 $P_{n + 1}$ 내에서 어떤 $p$ 와 $q$ 사이에 있어 $p < r < q$ 를 만족한다.

귀납가정에 따라 $U_{p}, U_{q}$ 는 이미 정의되어 있고 $\overline{U_{p}} \subset U_{q}$ 이다. 정규성을 사용하여 다음 조건을 만족하는 열린집합 $U_{r}$ 를 정의할 수 있다.

\overline{U_{p}} \subset U_{r}, \overline{U_{r}} \subset U_{q} .

이제 우리는 조건 $(*)$ 이 $P_{n + 1}$ 의 모든 쌍에 대해 성립함을 주장한다. 만약 비교되는 두 원소가 모두 $P_{n}$ 에 속한다면, 귀납가정에 의해 조건이 성립한다. 한 원소가 $r$ 이고 다른 하나가 $P_{n}$ 의 원소 $s$ 일 경우.

만약 $s \leq p$ 이면,

\overline{U_{s}} \subset \overline{U_{p}} \subset U_{r}

반대로 $s \geq q$ 이면,

\overline{U_{r}} \subset U_{q} \subset U_{s}

이로써 조건 $(*)$ 은 $P_{n + 1}$ 의 모든 쌍에 대해 성립하게 된다.

따라서 $P_{n + 1}$ 의 모든 쌍에 대해 조건 $(*)$ 이 성립하게 된다. 귀납법에 의해 이제 $P$ 의 모든 유리수 $p$ 에 대해 $U_{p}$ 가 정의되었다.

설명을 돕기 위해, 유리수들을 다음과 같은 표준적인 순서로 나열했다고 가정하자.

P = {1, 0, \frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{1}{4}, \frac{3}{4}, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \dots}

우리가 먼저 $U_{0}$ 와 $U_{1}$ 을 정의한 다음에는, $\overline{U_{0}} \subset U_{1/2}$ 이고 $\overline{U_{1/2}} \subset U_{1}$ 이 되도록 $U_{1/2}$ 를 정의하게 된다. 그 다음으로는 $U_{1/3}$ 을 $U_{0}$ 와 $U_{1/2}$ 사이에 적절히 넣고, $U_{2/3}$ 은 $U_{1/2}$ 와 $U_{1}$ 사이에 위치하도록 설정한다. 이와 같은 방식으로 계속해서 진행하며, 증명의 여덟 번째 단계에서는 그림과 같은 상황이 만들어지고, 아홉 번째 단계에서는 $U_{2/5}$ 를 $U_{1/3}$ 과 $U_{1/2}$ 사이에 맞춰 넣는 열린집합으로 택하게 된다. 이와 같은 과정을 반복한다.

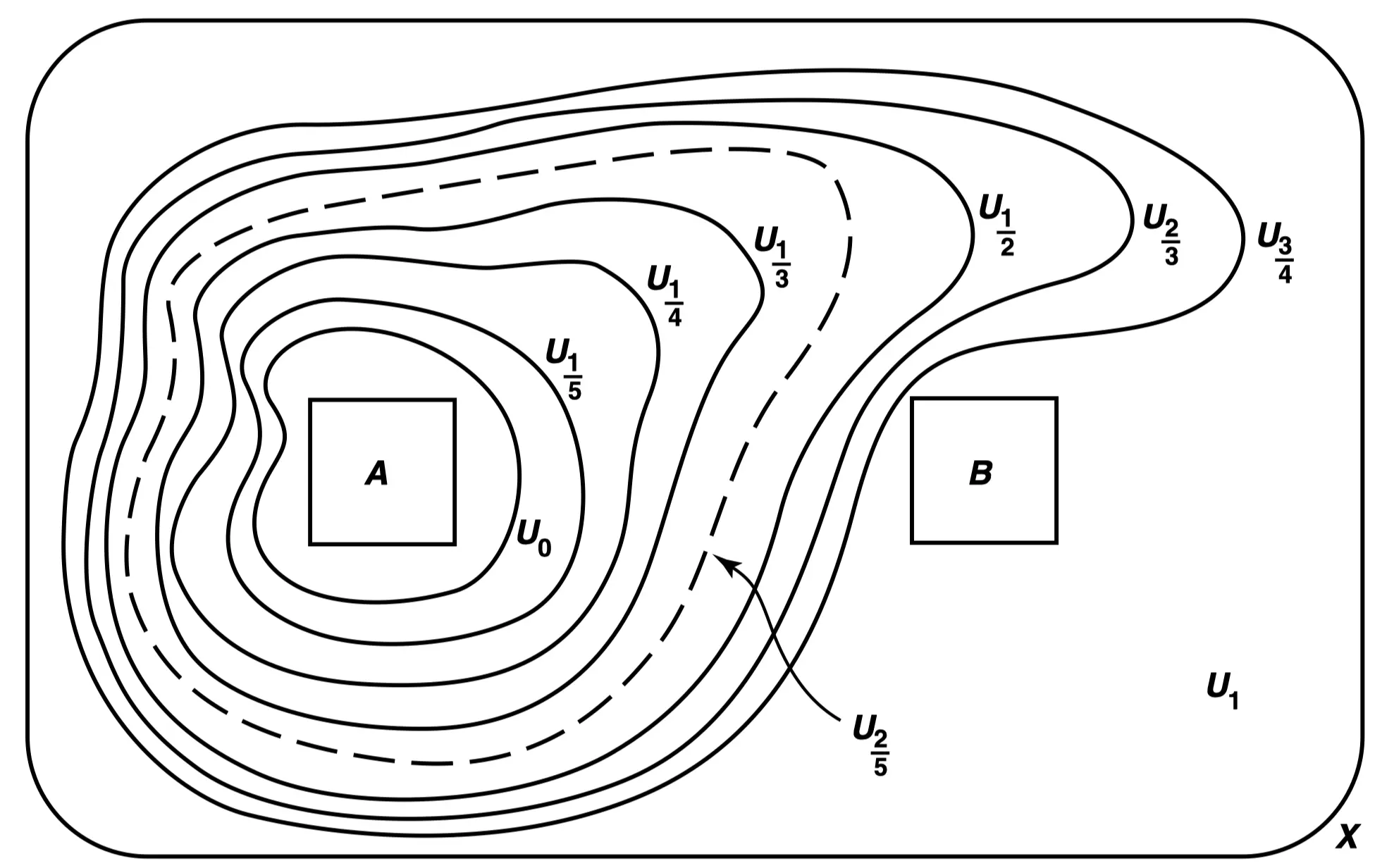
Step 2.

이제 우리는 구간 $[0, 1]$ 안의 모든 유리수 $p$ 에 대해 $U_{p}$ 를 정의하였다. 이제 이를 실수 전체에 속한 유리수 $p \in Q$ 에 대해 다음과 같이 확장한다.

U_{p} = \emptyset (if p < 0), U_{p} = X (if p > 1)

이 확장 정의 하에서도 여전히 다음 조건은 성립한다 (직접 확인할 수 있다).

p < q \Rightarrow \overline{U_{p}} \subset U_{q}

Step 3.

이제 $X$ 의 점 $x$ 에 대해 다음과 같은 집합 $Q (x)$ 를 정의하자. $Q (x)$ 는 $x \in U_{p}$ 가 되는 유리수 $p$ 들의 집합이다.

Q (x) = {p \in Q ∣ x \in U_{p}}

이 집합에는 0보다 작은 유리수는 포함되지 않는다. 왜냐하면 $p < 0$ 일 때 $U_{p} = \emptyset$ 이므로 $x$ 가 그 안에 포함될 수 없기 때문이다. 또한 이 집합에는 1보다 큰 모든 유리수가 포함된다. 왜냐하면 $p > 1$ 일 때 $U_{p} = X$ 이므로 모든 $x$ 가 포함되기 때문이다.

따라서 $Q (x)$ 는 $[0, 1]$ 안에 하계가 존재하는 집합이며, 그 최대 하계는 $[0, 1]$ 안의 어떤 실수이다. 이 값을 다음과 같이 정의하자.

f (x) = in f Q (x) = in f {p \in Q ∣ x \in U_{p}}

Step 4.

이제 $f$ 가 우리가 원하는 함수임을 보이자. 먼저 $x \in A$ 일 경우, $p \geq 0$ 인 모든 유리수에 대해 $x \in U_{p}$ 이므로 $Q (x)$ 는 0 이상인 모든 유리수로 구성된다. 따라서

f (x) = in f Q (x) = 0

반면 $x \in B$ 이면, $p \leq 1$ 인 어떤 $p$ 에 대해서도 $x \in / U_{p}$ 이므로 $Q (x)$ 는 1보다 큰 유리수들로만 구성되며

f (x) = 1

여기까지는 쉽다. 가장 어려운 부분은 $f$ 가 연속함수임을 보이는 것이다. 이를 위해, 다음의 기본 성질 두 가지를 먼저 증명한다.

$x \in \overline{U_{r}} \Rightarrow f (x) \leq r$
$x \in / U_{r} \Rightarrow f (x) \geq r$

1번 증명

$x \in \overline{U_{r}}$ 이면, $r < s$ 인 모든 $s$ 에 대해 $x \in U_{s}$ 가 되어야 하므로, $Q (x)$ 는 $r$ 보다 큰 모든 유리수를 포함한다

f (x) = in f Q (x) \leq r

2번 증명

$x \in / U_{r}$ 이면, $s < r$ 인 모든 $s$ 에 대해서도 $x \in / U_{s}$ 이므로 $Q (x)$ 는 $r$ 보다 작은 유리수를 포함하지 않는다.

f (x) = in f Q (x) \geq r

이제 $f$ 의 연속성을 증명하자. $X$ 의 한 점 $x_{0}$ 와, 실수 $R$ 안의 열린구간 $(c, d)$ 가 주어졌고, $f (x_{0}) \in (c, d)$ 라 하자. 우리는 $x_{0}$ 의 근방 $U$ 를 찾아서 $f (U) \subset (c, d)$ 가 되게 할 것이다.

실수 $c < p < f (x_{0}) < q < d$ 인 유리수 $p, q$ 를 잡는다. 이때 열린집합

U = U_{q} ∖ \overline{U_{p}}

는 $x_{0}$ 의 근방이 되며, 이 $U$ 에 속한 모든 점 $x$ 에 대해 $f (x) \in (c, d)$ 가 되도록 만들어진 것이다.

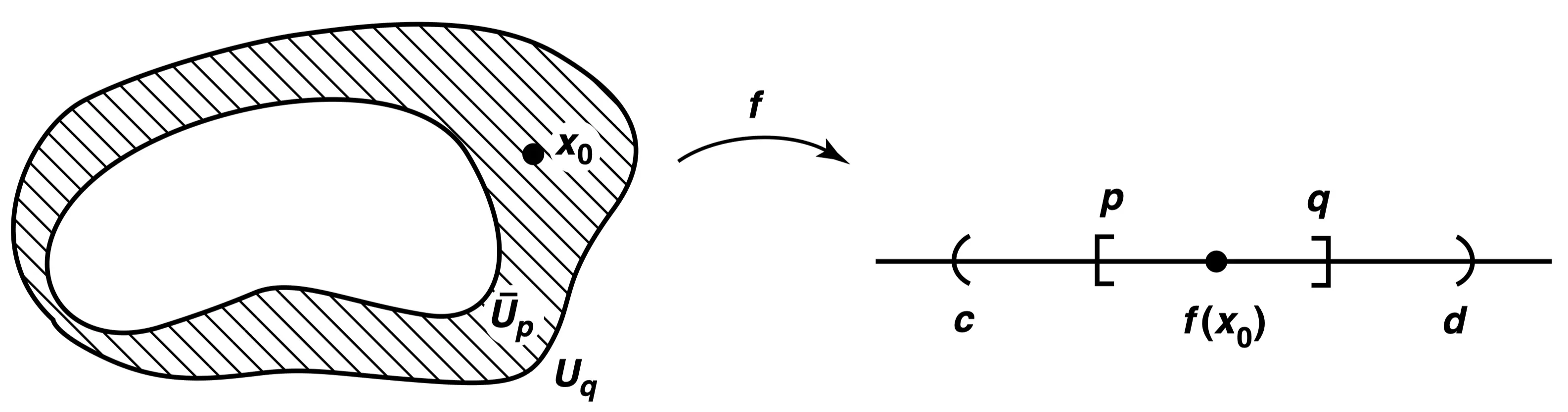
먼저, $x_{0} \in U$ 임을 확인하자. 이는 $f (x_{0}) < q$ 라면 조건 (2)에 의해 $x_{0} \in U_{q}$ , 그리고 $f (x_{0}) > p$ 라면 조건 (1)에 의해 $x_{0} \in / \overline{U_{p}}$ 이므로 자명하다.

다음으로, $f (U) \subset (c, d)$ 임을 보이자. $x \in U$ 인 점을 하나 택하자. 그러면 $x \in U_{q} \subset \overline{U_{q}}$ 이므로 조건 (1)에 의해 $f (x) \leq q$ 이다. 또한 $x \in / \overline{U_{p}}$ 이므로 $x \in / U_{p}$ , 따라서 조건 (2)에 의해 $f (x) \geq p$ 이다. 결국,

f (x) \in [p, q] \subset (c, d)

가 되어, 원하는 결과를 얻는다.

정의

위상공간 $X$ 의 두 부분집합 $A, B$ 가 주어졌을 때, 만약 $f : X \to [0, 1]$ 인 연속함수 $f$ 가 존재하여

f (A) = {0}, f (B) = {1}

이 되면, 우리는 $A$ 와 $B$ 가 연속함수에 의해 분리될 수 있다(can be separated by a continuous function)고 말한다.

Ray

Explorer