우리는 이 절에서 표면에 대한 우리 분류 정리의 기하학적 부분을 증명한다. 우리는 다각형 영역(polygonal region)의 변들을 쌍으로 붙여서 얻은 모든 공간이 나, 겹 원환면(n-fold torus) 이나, 또는 겹 사영 평면(m-fold projective plane) 중 하나와 위상동형(homeomorphic)임을 보인다. 나중에 우리는 모든 콤팩트 표면(compact surface)이 이런 방식으로 얻어질 수 있다는 문제를 논의할 것이다.
가 다각형 영역 에 대한 라벨링 계획(labelling scheme)이라 하자. 만약 각 라벨링이 이 계획에 정확히 두 번 나타나면, 우리는 그것을 적절한 라벨링 계획(proper labelling scheme) 이라 부른다. 다음의 중요한 사실에 주목하자:
적절한 계획에 어떤 기본 연산(elementary operation)을 적용하더라도, 또 다른 적절한 계획을 얻는다.
정의
를 단일 다각형 영역에 대한 적절한 라벨링 계획이라 하자. 만약 그 안의 각 라벨링이 한 번은 지수 로 나타나고 한 번은 지수 로 나타나면, 를 원환면 유형(torus type) 이라 말한다. 그렇지 않으면, 를 사영 유형(projective type) 이라 말한다.
우리는 사영 유형의 계획 를 고려하는 것부터 시작한다. 우리는 가 같은 지수를 가진 모든 라벨링들이 쌍을 이루어 계획의 시작 부분에 나타나는 (같은 길이의) 계획과 동치임을 보일 것이다. 즉, 는
형태의 계획과 동치이며, 여기서 은 원환면 유형이거나 비어있다.
가 사영 유형이므로, 에 있는 두 번의 등장이 모두 같은 지수를 갖는 라벨링, 가령 가 적어도 하나 존재한다. 따라서, 우리는 가
형태를 갖는다고 가정할 수 있으며, 여기서 중 일부는 비어 있을 수 있다. 이 표현에서 시각적 편의를 위해 괄호를 삽입하여,
로 쓸 것이다. 우리는 다음 결과를 갖는다:
보조정리 77.1
가
형태의 적절한 계획이라 하자. 여기서 중 일부는 비어 있을 수 있다. 그러면
라는 동치 관계가 성립하며, 여기서 은 의 형식적 역(formal inverse)을 나타낸다.
증명
1단계. 먼저 가 비어 있는 경우를 고려한다. 우리는
임을 보인다. 만약 이 비어 있으면 이 결과는 즉각적이며, 만약 가 비어 있으면 뒤집기(flipping), 순열(permuting), 라벨링 바꾸기(relabelling)에 의해 따라 나온다. 만약 둘 다 비어 있지 않다면, 그림에 나타난 자르고 붙이기(cutting and pasting) 논증을 적용하고, 그 후에 라벨링을 바꾼다. 관련된 기본 연산의 순서를 적는 것은 독자에게 맡긴다.
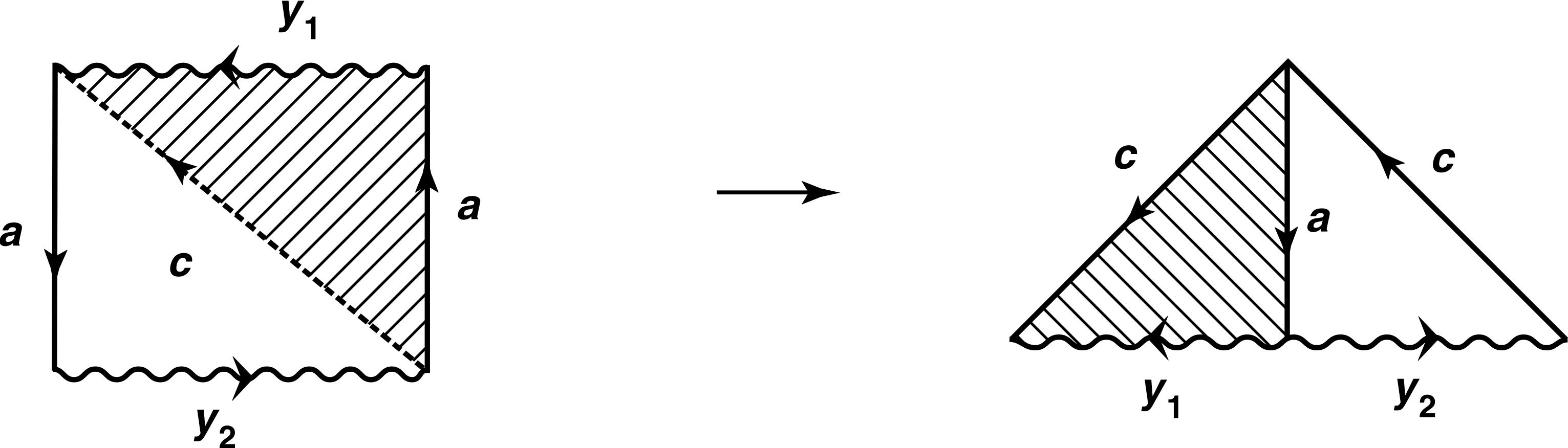
2단계. 이제 일반적인 경우를 고려한다. 라 하고, 여기서 는 비어 있지 않다. 만약 과 가 모두 비어 있다면, 보조정리는 순열에 의해 따라 나온다.
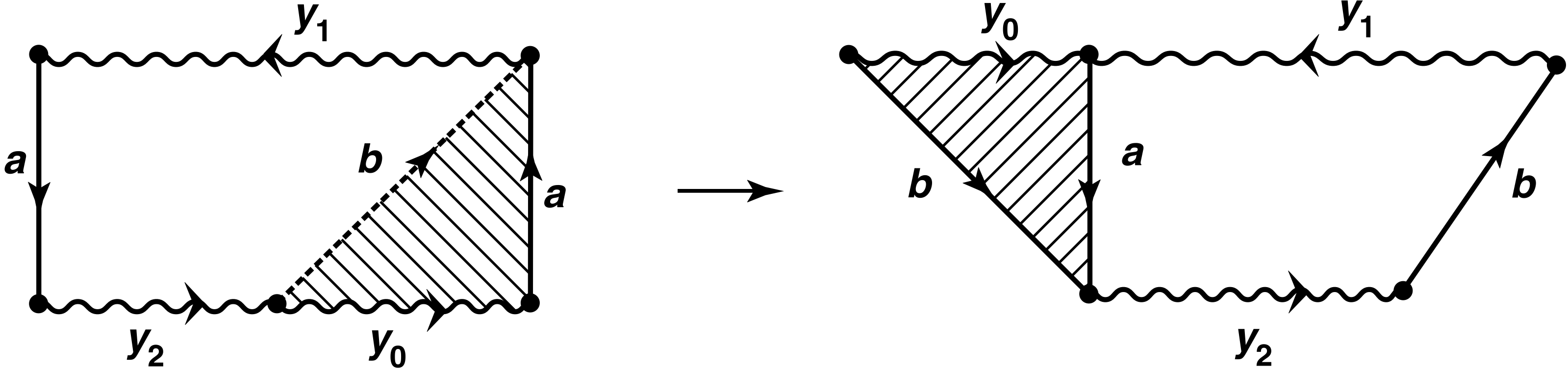
그렇지 않으면, 그림에 나타난 자르고 붙이기 논증을 적용하여
임을 보인다. 이로부터
이 성립한다.
보조정리 77.2
만약 가 사영 유형의 계획이라면, 는
형태의 같은 길이를 갖는 계획과 동치이며, 여기서 이고 은 비어 있거나 원환면 유형이다.
증명
계획 는
형태로 쓸 수 있다. 그러면 앞선 보조정리는 가 와 같은 길이를 갖는 형태의 계획과 동치임을 암시한다. 만약 이 원환면 유형이면, 증명은 끝난다. 그렇지 않으면, 를
형태로 쓸 수 있다. 앞선 보조정리를 다시 적용하면, 가
형태의 계획 과 동치라고 결론 내릴 수 있으며, 여기서 은 와 같은 길이를 갖는다. 만약 가 원환면 유형이면, 증명은 끝난다. 그렇지 않으면, 논증을 유사하게 계속한다.
앞선 보조정리로부터, 만약 가 다각형 영역에 대한 적절한 라벨링 계획이라면, (1) 는 원환면 유형이거나, (2) 는 형태의 계획과 동치이며, 여기서 은 원환면 유형이거나, (3) 는 형태의 계획과 동치이다. 경우 (3)에서는, 그러한 계획은 사영 평면들의 연결합을 나타내므로 증명이 끝난다. 따라서 경우 (1)과 (2)를 고려하자.
이 시점에서, 만약 가 경우 (1) 또는 (2)에 나타난 형태이고 길이가 4보다 크며, 같은 라벨링을 가지지만 반대 지수를 갖는 두 인접한 항을 포함한다면, 상쇄 연산이 적용되어 를 더 짧은 계획으로 줄일 수 있으며, 이 역시 경우 (1), (2), 또는 (3)에 나타난 형태이다. 따라서, 우리는 를 길이가 4인 계획이나, 그러한 두 인접한 항을 포함하지 않는 계획으로 줄일 수 있다.
길이가 4인 계획은 나중에 볼 것처럼 다루기 쉽다. 따라서 가 같은 라벨링을 가지지만 반대 지수를 갖는 두 인접한 항을 포함하지 않는다고 가정하자. 그 경우, 가 와 같은 길이를 가지며
형태를 갖는 계획 과 동치임을 보인다. 여기서 은 원환면 유형이거나 비어있다. 이것이 다음 보조정리의 내용이다.
보조정리 77.3
를 형태의 적절한 계획이라 하자. 여기서 은 같은 라벨링을 가진 두 인접한 항을 포함하지 않는 원환면 유형의 계획이다. 그러면 는 형태의 계획과 동치이며, 여기서 는 과 같은 길이를 갖고
형태를 갖는다. 여기서 은 원환면 유형이거나 비어있다.
증명
이것은 이 절에서 가장 정교한 증명이다; 세 번의 자르고 붙이기가 포함된다. 우리는 먼저, 라벨링과 지수를 바꾸면 필요에 따라 를
형태로 쓸 수 있음을 보인다. 여기서 중 일부는 비어 있을 수 있다.
에 나타나는 라벨링들 중에서, (물론 반대 지수를 가진) 두 번의 등장이 가능한 한 서로 가까이 있는 라벨링 를 택하자. 이 등장들은 가정에 의해 인접하지 않다. 필요하다면 지수를 바꾸어, 항 가 먼저 나타나고 항 이 두 번째로 나타난다고 가정할 수 있다. 와 사이에 나타나는 어떤 라벨링 를 택하고, 그 지수가 이라고 가정할 수 있다. 이제 항 은 에 나타나지만, 와 이 가능한 한 가깝기 때문에 이 둘 사이에는 나타날 수 없다. 만약 이 뒤에 나타난다면, 증명은 끝난다. 만약 그것이 앞에 나타난다면, 우리가 해야 할 일은 항들의 지수를 바꾸고, 그 다음 라벨링 와 를 바꾸어 원하는 형태의 계획을 얻는 것이다.
따라서 가 형태를 갖는다고 가정하자.
첫 번째 자르고 붙이기. 가 계획
와 동치임을 보인다. 이 결과를 증명하기 위해, 를
형태로 다시 쓴다. 그 다음 그림 77.3에 나타난 자르고 붙이기 논증을 적용하여
라고 결론짓는다. 이는 라벨링을 바꾼 것이다. 에서의 자르기는 결과적인 두 다각형이 모두 적어도 세 개의 변을 가지기 때문에 가능하다는 점에 주목하자.
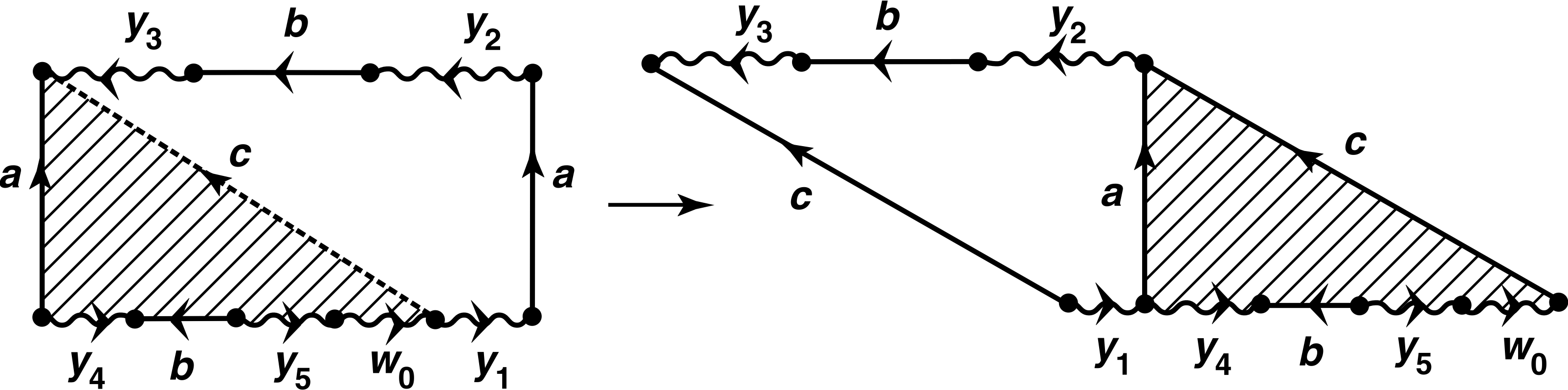
두 번째 자르고 붙이기.
가 주어졌을 때, 이 계획
와 동치임을 보인다. 만약 모든 계획 와 가 비어 있다면, 논증은 쉽다. 왜냐하면 그 경우
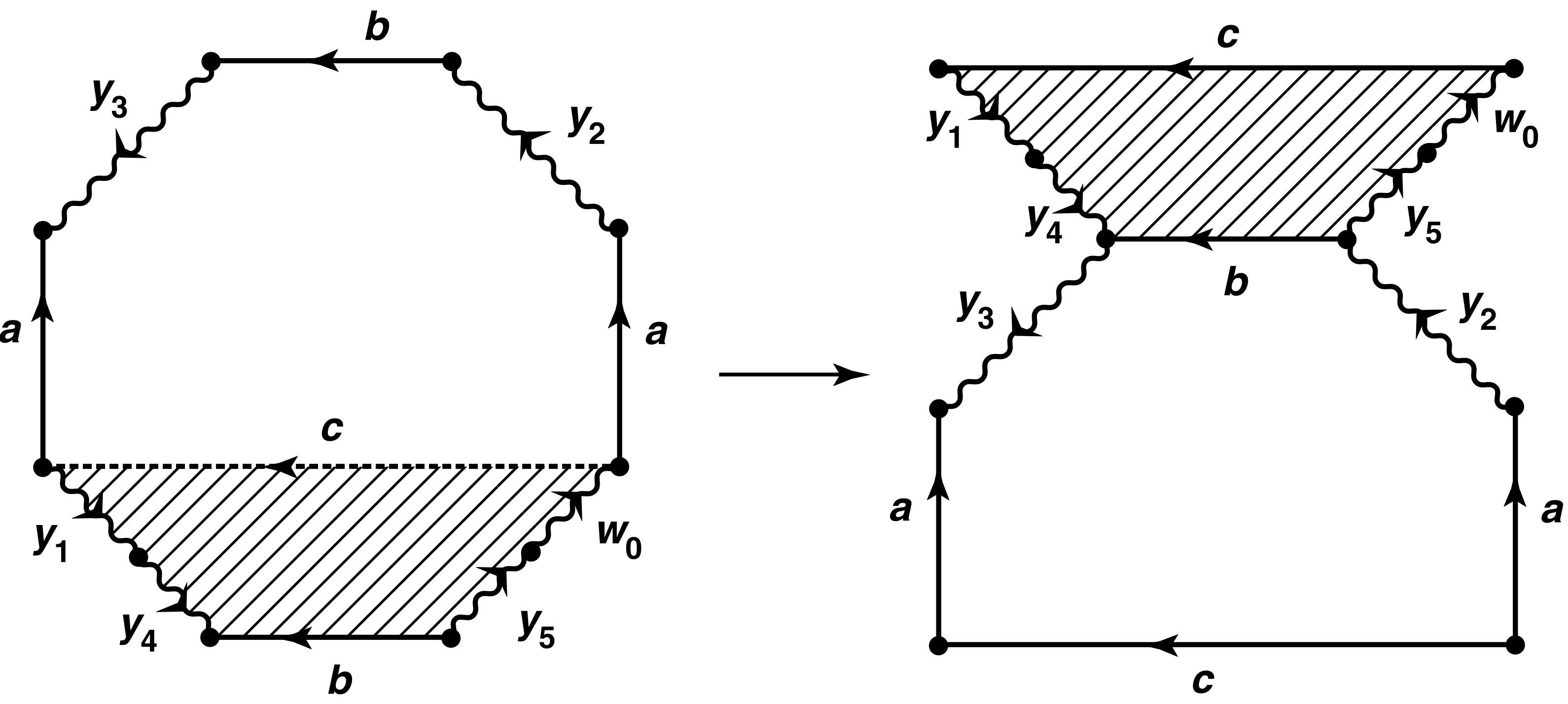
이기 때문이다. 그렇지 않으면, 그림에 나타난 논증을 적용하여
라고 결론짓는다. 이는 라벨링을 바꾼 것이다.
세 번째 자르고 붙이기. 증명을 완성한다.
가 주어졌을 때, 이 계획
와 동치임을 보인다. 만약 계획 가 비어 있다면, 논증은 쉽다. 왜냐하면 그 경우
이기 때문이다. 그렇지 않으면, 그림에 나타난 논증을 적용하여
라고 결론짓는다. 이는 라벨링을 바꾼 것이며 원하는 결과이다.

분류 절차의 마지막 단계는 사영 평면들과 원환면들의 연결합이 사영 평면들만의 연결합과 동치임을 보이는 것이다.
보조정리 77.4
를
형태의 적절한 계획이라 하자. 그러면 는 계획
과 동치이다.
증명
적절한 계획에 대해
가 성립함을 보조정리 77.1에서 상기하자. 우리는 다음과 같이 진행한다:
정리 77.5 (분류 정리, The classification theorem)
가 평면의 다각형 영역으로부터 그 변들을 쌍으로 붙여서 얻은 몫공간이라 하자. 그러면 는 , 겹 원환면 , 또는 겹 사영 평면 중 하나와 위상동형이다.
증명
를 공간 를 다각형 영역 로부터 형성하는 라벨링 계획이라 하자. 그러면 는 길이가 최소 4인 적절한 계획이다. 우리는 가 다음 계획들 중 하나와 동치임을 보인다:
- (단, )
- (단, )
첫 번째 계획은 §74의 예제 2와 4에서 언급했듯이 공간 를, 두 번째 계획은 공간 를 낳는다. 세 번째는 공간 으로, 네 번째는 공간 으로 이어진다.
1단계. 를 원환면 유형의 적절한 계획이라 하자. 우리는 가 계획 (1) 또는 계획 (4) 유형 중 하나와 동치임을 보인다. 만약 의 길이가 4라면, 이는
형태 중 하나로 쓰여질 수 있다. 첫 번째는 (1) 유형이고 두 번째는 (4) 유형이다. 우리는 의 길이에 대한 귀납법으로 진행한다. 의 길이가 4보다 크다고 가정하자. 만약 가 더 짧은 원환면 유형의 계획과 동치라면, 귀납적 가정이 적용된다. 그렇지 않으면, 우리는 가 같은 라벨링을 가진 인접한 두 항을 포함하지 않음을 안다. 우리는 보조정리 77.3 (단, 는 비어 있음)을 적용하여 가
형태의 와 같은 길이를 갖는 계획과 동치라고 결론 내린다. 여기서 은 원환면 유형이다. 의 길이가 4보다 크므로 은 비어 있지 않다. 다시, 가 더 짧은 원환면 유형의 계획과 동치이지 않으므로, 은 같은 라벨링을 가진 두 인접한 항을 포함할 수 없다. 보조정리를 다시 적용하면, 로 하여, 가
형태의 계획과 동치라고 결론 내린다. 여기서 는 비어 있거나 원환면 유형이다. 만약 가 비어 있다면, 증명은 끝난다. 그렇지 않으면, 보조정리를 다시 적용한다. 유사하게 계속한다.
2단계. 이제 를 사영 유형의 적절한 계획이라 하자. 우리는 가 계획 (2) 또는 계획 (3) 유형 중 하나와 동치임을 보인다. 만약 의 길이가 4라면, 보조정리 77.2는 가 계획 또는 중 하나와 동치임을 암시한다. 첫 번째는 (3) 유형이다. 두 번째는 인 형태로 쓸 수 있다. 그러면 보조정리 77.1은 그것이 계획 와 동치임을 암시하며, 이는 (2) 유형이다. 우리는 의 길이에 대한 귀납법으로 진행한다. 의 길이가 4보다 크다고 가정하자. 보조정리 77.2는 가
형태의 계획과 동치라고 말한다. 여기서 이고 은 원환면 유형이거나 비어있다. 만약 이 비어 있다면, 증명은 끝난다. 만약 이 같은 라벨링을 가진 두 인접한 항을 가진다면, 는 더 짧은 사영 유형의 계획과 동치이며 귀납적 가정이 적용된다. 그렇지 않으면, 보조정리 77.3은 가
형태의 계획과 동치라고 말한다. 여기서 는 비어 있거나 원환면 유형이다. 그러면 우리는 보조정리 77.4를 적용하여 이 계획
와 동치라고 결론 내린다. 우리는 유사하게 계속한다. 결국 우리는 (3) 유형의 계획에 도달한다.