분류 정리를 증명하기 위해, 우리는 “자르고 붙이기” 기법이라 불리는 특정 기하학적 논증을 사용해야 한다. 이 기법들은 어떤 라벨링 계획(labelling scheme)에 따라 하나 이상의 다각형 영역(polygonal regions)의 변들을 붙여서 얻은 공간 를 가져와서, 다른 다각형 영역들의 모음과 다른 라벨링 계획(labelling scheme)으로 를 표현하는 방법을 보여준다.
먼저, 다각형 영역을 “잘라 나누는 것”이 무엇을 의미하는지 생각해 보자. 를 평소와 같이 연속적인 꼭짓점 을 갖는 다각형 영역이라 하자. 인 주어진 에 대해, 연속적인 꼭짓점 을 갖는 다각형 영역 과 연속적인 꼭짓점 을 갖는 다각형 영역 를 생각하자. 이 영역들은 변 를 공통으로 가지며, 영역 는 그들의 합집합이다.
이제 의 평행이동(translation)으로 을 움직여 와 서로소(disjoint)인 다각형 영역 을 얻자. 그러면 은 연속적인 꼭짓점 을 가지며, 여기서 는 평행이동 하에서 의 상이다. 영역 과 는 에서 로 가는 선을 따라 를 잘라 얻었다고 말한다. 영역 는 의 에서 로 가는 변을 의 에서 로 가는 변에 양의 선형 사상(positive linear map)으로 붙여서 얻은 과 의 몫공간(quotient space)과 위상동형(homeomorphic)이다.

이제 이 과정을 어떻게 되돌릴 수 있는지 생각해 보자. 연속적인 꼭짓점 을 갖는 과 연속적인 꼭짓점 을 갖는 라는 두 서로소 다각형 영역이 주어졌다고 하자. 그리고 의 에서 로 가는 변을 의 에서 로 가는 변에 양의 선형 사상으로 붙여서 몫공간을 형성한다고 하자. 우리는 이 공간을 다각형 영역 로 표현하고 싶다.
이 작업은 다음과 같이 수행된다: 의 점들은 원 위에 있으며 시계 반대 방향으로 배열되어 있다. 가 시계 반대 방향 순서로 배열되도록 이 동일한 원 위에 점 들을 선택하고, 이들을 연속적인 꼭짓점으로 하는 다각형 영역을 이라 하자. 를 로 보내고 의 변 를 의 변 위로 선형으로 사상하는 에서 으로의 위상동형사상이 존재한다. 따라서, 문제의 몫공간은 과 의 합집합인 영역 와 위상동형이다. 우리는 가 과 를 표시된 변들을 따라 붙여서 얻어졌다고 말한다.
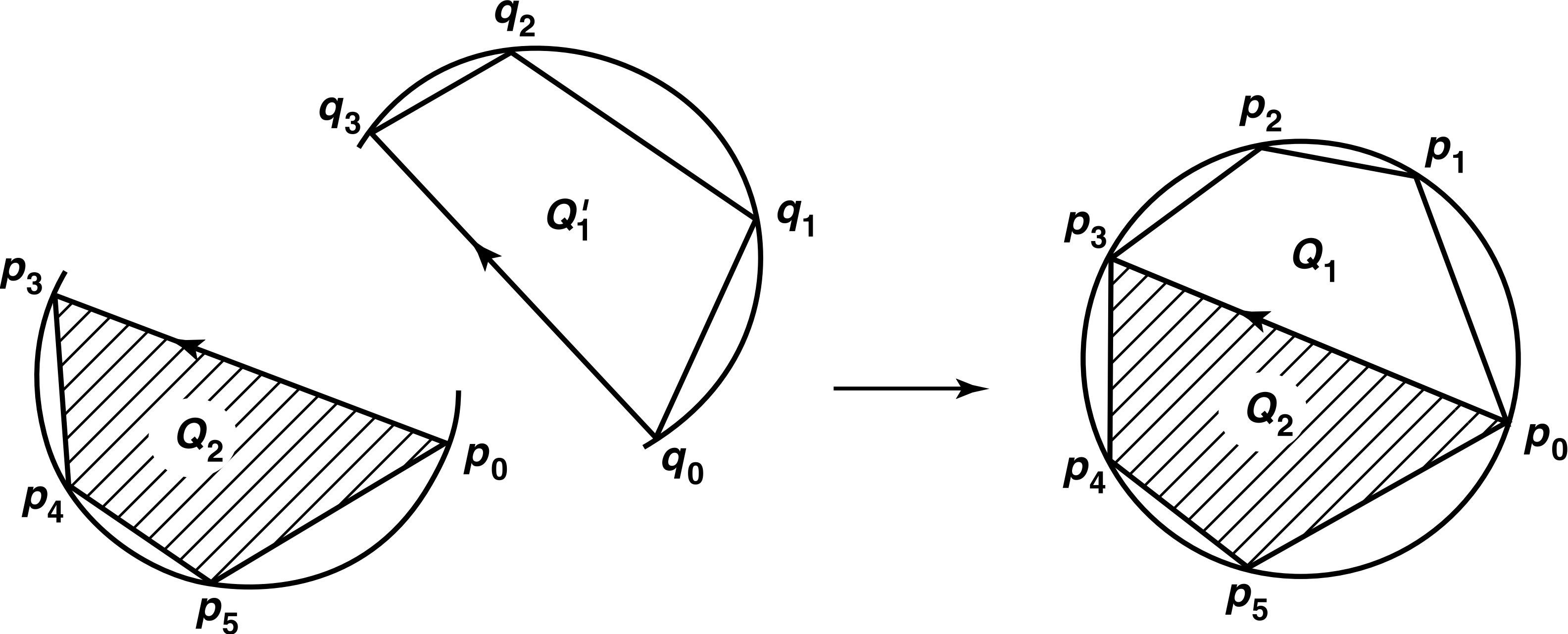
이제 다음 질문을 던져보자: 다각형 영역에 라벨링 계획이 있을 때, 영역을 잘라 나누는 것이 이 라벨링 계획에 어떤 영향을 미치는가? 더 정확하게, 서로소인 다각형 영역들의 모음 과 이 영역들에 대한 라벨링 계획 이 있다고 하자. 여기서 는 의 변들에 대한 라벨링 계획이다. 가 이 라벨링 계획으로부터 얻어진 몫공간이라고 하자. 만약 우리가 을 에서 로 가는 선을 따라 잘라 나눈다면, 무슨 일이 일어나는가? 우리는 개의 다각형 영역 을 얻는다. 이 영역들로부터 공간 를 얻기 위해서는 하나의 추가적인 변 붙이기가 필요하다. 우리는 우리가 도입한 변 와 에 할당될 새로운 라벨링을 도입함으로써 필요한 추가적인 붙이기를 표시한다. 에서 로의 방향이 에 대해 시계 반대 방향이고, 에서 로의 방향이 에 대해 시계 방향이므로, 이 라벨링은 의 계획에 나타날 때 지수 을 가지고, 의 계획에 나타날 때 지수 을 가질 것이다.
좀 더 구체적으로 말하자면, 에 대한 라벨링 계획 을 형태로 쓸 수 있다. 여기서 는 의 첫 개 항으로 구성되고, 은 나머지로 구성된다. 를 어떤 계획 에도 나타나지 않는 라벨링이라 하자. 그러면 에는 라벨링 계획 을, 에는 라벨링 계획 을 부여하고, 인 에는 이전의 계획 를 부여한다.
이 라벨링 계획을 통해 공간 가 영역 으로부터 얻어질 수 있다는 것은 자명하다. 왜냐하면 몫 사상의 합성은 몫 사상이므로, 모든 변들을 한 번에 붙이든, 아니면 다른 변들을 붙이기 전에 변 를 변 에 붙이든 상관없기 때문이다!
물론 이 절차를 역으로 적용할 수도 있다. 만약 가 영역 에 대한 라벨링 계획으로 표현되고, 라벨링 계획이 첫 번째 영역의 변이 두 번째 영역의 변에 붙여져야 함을 나타내고(그리고 다른 어떤 변도 이 변들에 붙여지지 않는다면), 우리는 실제로 붙이기를 수행하여 를 개의 영역 에 대한 라벨링 계획으로 표현할 수 있다.
이 사실을 공식적으로 정리로 기술한다:
정리 76.1
가 라벨링 계획
에 따라 개의 다각형 영역의 변들을 붙여서 얻은 공간이라 하자. 를 이 계획에 나타나지 않는 라벨링이라 하자. 만약 와 이 모두 길이가 최소 2라면, 는 또한 개의 다각형 영역의 변들을 계획
에 따라 붙여서 얻을 수도 있다.
역으로, 가 계획 에 의해 개의 다각형 영역으로부터 얻은 공간이라면, 가 계획 에 나타나지 않는다는 조건 하에, 개의 다각형 영역으로부터 계획 에 의해 얻어질 수도 있다.
계획에 대한 기본 연산 (Elementary operations on schemes)
이제 우리는 결과적인 몫공간 에 영향을 주지 않고 라벨링 계획 에 수행할 수 있는 여러 기본 연산들을 나열한다. 처음 두 가지는 방금 언급한 정리로부터 나온다.
(i) 자르기 (Cut). 계획 을 계획 과 으로 대체할 수 있다. 단, 가 전체 계획의 다른 곳에 나타나지 않고 와 의 길이가 최소 2여야 한다.
(ii) 붙이기 (Paste). 계획 과 을 계획 으로 대체할 수 있다. 단, 가 전체 계획의 다른 곳에 나타나지 않아야 한다.
(iii) 라벨링 바꾸기 (Relabel). 주어진 어떤 라벨링의 모든 발생을 전체 계획의 다른 곳에 나타나지 않는 다른 라벨링으로 대체할 수 있다. 유사하게, 주어진 라벨링 의 모든 발생의 지수의 부호를 바꿀 수 있다. 이는 ""로 라벨링된 모든 변의 방향을 뒤집는 것에 해당한다. 이 두 변경 모두 붙이기 사상에 영향을 주지 않는다.
(iv) 순열 (Permute). 계획 중 하나를 의 순환 순열(cyclic permutation)로 대체할 수 있다. 구체적으로, 이면, 를 로 대체할 수 있다. 이는 다각형 영역 의 꼭짓점들을 다른 꼭짓점에서 시작하도록 번호를 다시 매기는 것에 해당하며, 결과적인 몫공간에는 영향을 주지 않는다.
(v) 뒤집기 (Flip). 계획
을 그 형식적 역(formal inverse)
으로 대체할 수 있다. 이는 단순히 다각형 영역 를 “뒤집는 것”에 해당한다. 꼭짓점의 순서가 반대가 되고, 각 변의 방향도 반대가 된다. 몫공간 는 영향을 받지 않는다.
(vi) 상쇄 (Cancel). 계획 을 계획 으로 대체할 수 있다. 단, 가 전체 계획의 다른 곳에 나타나지 않고 와 의 길이가 최소 2여야 한다.
이 마지막 결과는 그림에 나타난 3단계 논증으로부터 따라 나온다. 이 중 한 단계만이 새롭다. 와 를 전체 계획의 다른 곳에 나타나지 않는 라벨링라 하자. 먼저 자르기 연산 (i)를 사용하여 을 계획 와 으로 대체한다. 그 다음, 각 다각형 영역에서 와 로 라벨링된 변들을 새로운 라벨링를 가진 단일 변으로 결합한다. 이것이 새로운 단계이다. 결과는 계획 와 이며, 이를 붙이기 연산 (ii)를 사용하여 단일 계획 으로 대체할 수 있다.
(vii) 비상쇄 (Uncancel). 이것은 연산 (vi)의 역이다. 계획 을 계획 으로 대체한다. 여기서 는 전체 계획의 다른 곳에 나타나지 않는 라벨링이다. 우리는 실제로 이 연산을 사용할 기회는 없을 것이다.
정의
다각형 영역들의 모음에 대한 두 라벨링 계획이, 하나가 다른 하나로부터 기본 계획 연산들의 유한한 순서에 의해 얻어질 수 있을 때, 동치(equivalent) 라고 정의한다. 각 기본 연산은 그 역이 또 다른 그러한 연산이므로, 이것은 동치 관계(equivalence relation)이다.
예제 1
클라인 병(Klein bottle) 는 라벨링 계획 로부터 얻어지는 공간이다. §74의 연습문제에서, 가 2겹 사영 평면 와 위상동형임을 보이도록 요청받았다. 거기에 제시된 기하학적 논증은 사실상 다음과 같은 기본 연산들로 구성된다: