등차수열(Arithmetic sequence)

실수열

수열은 숫자의 나열로 자연수를 차례로 넣었을 때, 어떤 실수가 대응되는 구조다. 그러므로 수열은 자연수 $\mathbb{N}$을 정의역으로 하고 실수 $\mathbb{R}$을 공역으로 하는 함수다.

$$f:\mathbb{N}\to \mathbb{R}$$

등차수열 식의 이해

등차수열은 연속하는 항들 사이의 차이가 항상 일정한 수열이다.

$$a_{n+1}-a_n=d$$

이 수열을 자연수 $n$에 대한 함수로 바라보. 기울기는 기본적으로 두 점 사이의 $x$ 증가량분의 $y$ 증가량으로 정의된다.

$$\text{기울기}=\frac{\Delta y}{\Delta x}$$

등차수열 $a_1,a_2,a_3,\cdots$는 각각 항 번호 $n$에 대응되는 값이므로, 항 번호 $n$을 $x$값, 항 $a_n$을 $y$값으로 생각할 수 있다. 이 수열을 평면 상의 점 $(1,a_1),(2,a_2),(3,a_3),\cdots$으로 본다면, 이 점들은 모두 기울기가 일정한 직선 위에 놓이게 된다.

이때, 항 번호 $n$이 $1$씩 증가할 때마다, 항 $a_n$은 항상 공차 $d$만큼 증가한다.

$$\Delta x=1,\Delta y=d$$

그러므로 기울기는 $d$ 이다.

$$\frac{\Delta y}{\Delta x}=\frac{d}{1}=d$$

따라서 등차수열을 일차함수로 표현하면 최고차항의 계수는 공차 $d$가 된다.

등차수열 식의 응용

연속하는 두 항의 차이가 모두 일정한 수열 이때 두 항의 차이는 공통적으로 나타나는 차이므로 공차(common difference) 라고 한다.

$$\begin{array}{rl}{a}_n& =a_1+(n-1)d=dn+(a-d)\\ S_n& =\frac{a+l}{2}\times n=\frac{n}{2}\left\{2a+(n-1)d\right\}=\frac{d}{2}{n}^2+\left(a-\frac{d}{2}\right)n\end{array}$$

등차수열은 공차를 기울기로 갖는 일차함수이고 등차수열의 합은 등차수열을 적분한 꼴이므로 상수항이 없는 이차함수이다. 따라서 등차수열의 일반항을 구할 때는

$$a_n=dn+c$$

라 적은 후 양변에

$$n=1$$

을 대입하여 상수항을 보정한다. 같은 방법으로 등차수열의 합을 구할 때는

$$S_n=\frac{d}{2}{n}^2+cn$$

이라 적은 후 양변에

$$n=1$$

을 대입 하여 일차항의 계수를 보정한다.

예시

$3,5,7,9,\cdots$인 등차수열이 있을 때 등차수열의 일반항은 , $d=2$이므로 $a_n=2n+c$라 적은 후 $n=1$을 대입하면 $a_1=2+x$이고 $a_1=3$이므로 $x=1$이다. 따라서

$$a_n=2n+1$$

이라 구할 수 있다.

등차수열의 합은 $d=2$이므로

$$S_n=n^2+cn$$

이라 적은 후 $n=1$을 대입하면 $S_1=1+x$이고 $S_1=a_1=3$이므로 $c=2$이다. 따라서

$$S_n=n^2+2n$$

이라 구할 수 있다.

등차수열과 미적분의 관계

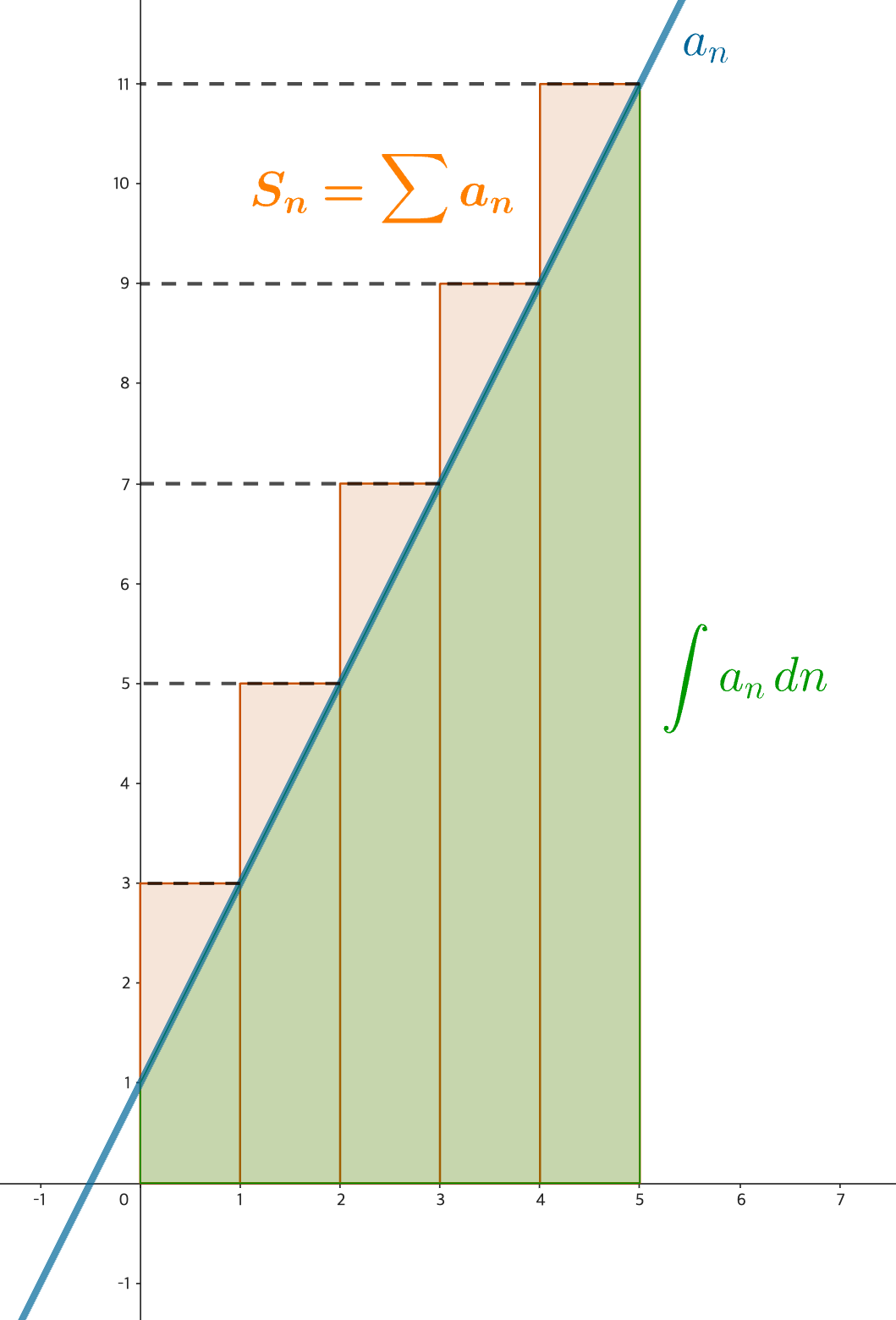
등차수열을 적분하면 등차수열의 합 꼴이 나오고 등차수열의 합을 미분하면 등차수열의 꼴이 나옴을 응용하면 등차수열로부터 등차수열의 합 또는 등차수열의 합으로부터 등차수열을 빠르게 찾을 수 있다.¹

예를 들어 $a_n=2n+1$을 적분한다 생각하고 최고차항만 적분하면

$$S_n=n^2+cn$$

이라 할 수 있다. $a_1=S_1=3$이므로 $c=2$이고 따라서, $S_n=n^2+2n$이다. 반대로

$$S_n=n^2+2n$$

을 미분한다 생각하고 최고차항만 미분하면

$$a_n=2n+c$$

라 할 수 있다. $a_1=S_1=3$이므로 $c=1$이고 따라서

$$a_n=2n+1$$

이다.

상수항이 있는 이차함수는 등차수열일까?

$S_n=n^2+2n+2$에 대하여 $a_n$의 각 항을 찾으면 다음과 같고 $a_n$은 첫째항을 제외하면 $a_n=2n+1$인 등차수열 꼴임을 알 수 있다.

$$\begin{array}{cc}{S}_1=5& a_1=5\\ S_2=10& a_2=5\\ S_3=17& a_3=7\\ S_4=26& a_4=9\\ S_5=37& a_5=11\\ ⋮& ⋮\end{array}$$

이는 상수항이 없다고 생각하면 앞선 방법과 같이 찾을 수 있다.

$$a_n=\{\begin{array}{l}{S}_1(n=1)\\ S_n-S_{n-1}(n>1)\end{array}$$

상수항이 있는 이차함수 $S_n$을 이용하여 $a_n$을 찾고 싶다면 상수항이 없다고 생각하고 $a_n$을 찾은 후, 첫째항은 따로 찾는 것을 추천한다.

Footnotes

1. 등차수열의 합이 함수의 정적분과 완전히 일치하지 않는 이유는 각 항마다 직사각형으로 근사한 합이 실제 함수 아래 면적보다 조금 더 크기 때문이다. 등차수열 $a_n=dn+c$를 연속함수 $a_x=dx+c$로 확장하고, 그 위에 오른쪽 끝점을 기준으로 한 밑변 1인 직사각형을 그리면 각 사각형은 정적분 면적보다 위로 살짝 튀어나온 부분을 갖게 된다. 이 튀어나온 부분은 사각형의 오른쪽 위 모서리와 함수 그래프 사이에 생긴 작은 삼각형이며, 그 삼각형의 밑변은 1이고 높이는 공차 $d$이므로 넓이는 $\frac{1}{2}\cdot 1\cdot d=\frac{d}{2}$이다. 이 삼각형이 $n$개 있으므로 전체 초과된 넓이는 $\frac{d}{2}n$이 되고, 따라서 등차수열의 합은 대응하는 정적분 값보다 항상 $\frac{d}{2}n$만큼 더 크다. 이 차이는 근사나 오차가 아니라, 이산적인 수열의 합과 연속적인 적분이 본질적으로 가지는 구조의 차이에서 발생한다. ↩