다항 함수의 넓이 공식

다항함수 $f(x)=a{x}^n+\cdots$ 와 직선 $x$축(또는 직선)으로 둘러싸인 넓이는 다음과 같이 표현할 수 있다. 평행이동 또는 치환적분을 이용하여 간단하게 표현할 수 있다.

이차함수

삼차함수

사차함수

이차함수 응용

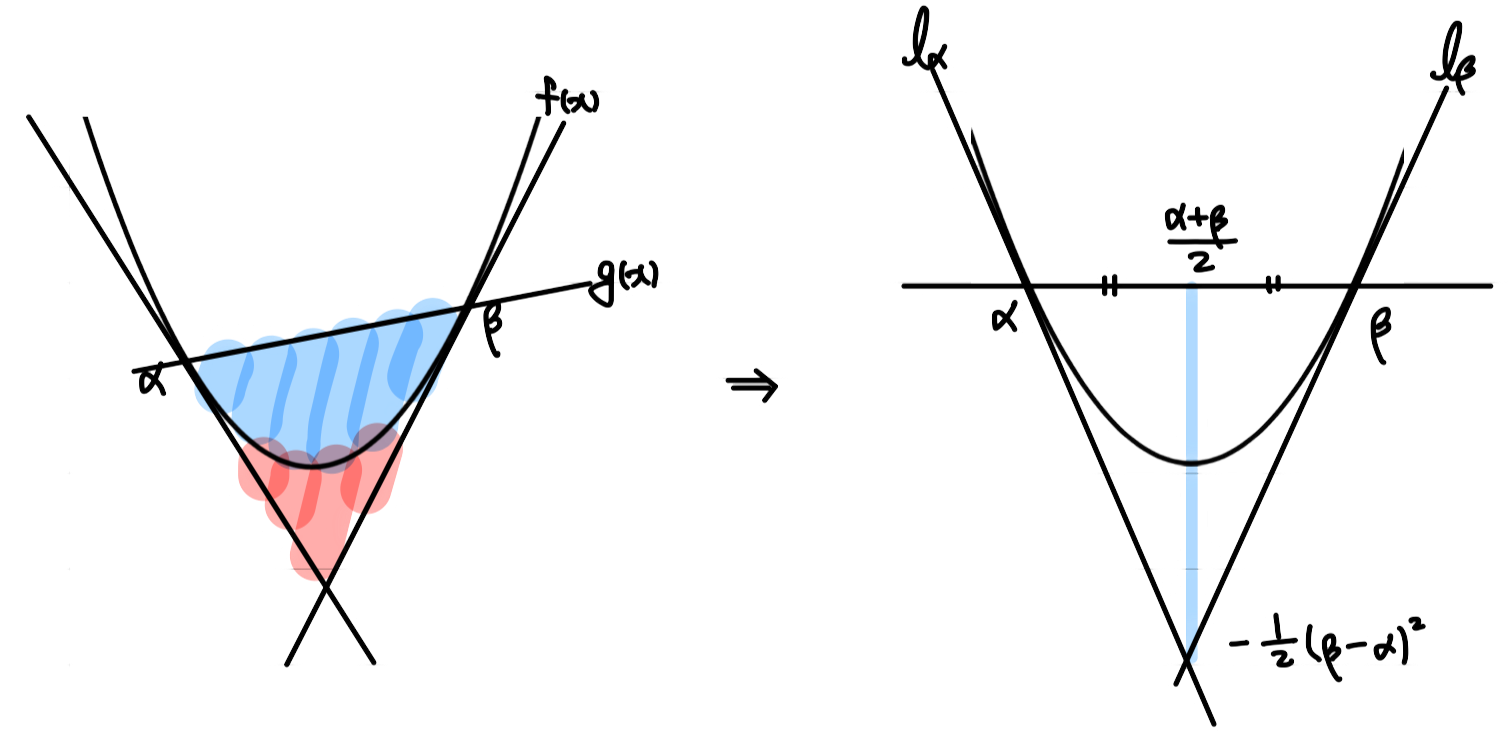
이차함수 $y=f(x)$에 그은 두 접선과 곡선 $f(x)$ 사이의 넓이 관계를 보자. 두 접점이 각각 $\alpha$와 $\beta$일 때, 이 두 접점을 잇는 직선의 방정식을 $g(x)$라고 하자.

$f(x)$는 이차함수, $g(x)$는 직선이므로 $f(x)-g(x)$는 두 교점 $\alpha ,\beta$를 지나는 이차함수가 된다. 이때, $f(x)-g(x)$는 $a(x-\alpha )(x-\beta )$ 형태로 표현될 수 있다. 여기서 $a$는 이차함수 $f(x)$의 최고차항 계수다.

• $l_{\alpha }$의 방정식: $y=(\alpha -f(\alpha ))(x-\alpha )$
• $l_{\beta }$의 방정식: $y=(\beta -f(\beta ))(x-\beta )$

두 접선 $l_{\alpha }$와 $l_{\beta }$의 교점은 $x=\frac{\alpha +\beta }{2}$일 때 발생하며, 이때 $y$ 값은 $-\frac{1}{2}(\beta -\alpha {)}^2$ 이다. 이는 두 접선의 교점의 좌표가 두 접점의 중점임을 나타낸다.

• 삼각형의 넓이: 두 접선과 $y$축 (혹은 $x=\frac{\alpha +\beta }{2}$ 직선)이 만드는 삼각형의 넓이는 $\frac{|\beta -\alpha {|}^3}{4}$
• 윗부분의 넓이: 두 접선 $l_{\alpha },l_{\beta }$와 곡선 $f(x)$로 둘러싸인 영역 중 윗부분(파랑)의 넓이는 $\frac{|\beta -\alpha {|}^3}{6}$
• 아랫부분의 넓이: 두 접선과 곡선으로 둘러싸인 영역 중 아랫부분(빨강)의 넓이는 $\frac{|\beta -\alpha {|}^3}{12}$

따라서 윗부분의 넓이와 아랫부분의 넓이의 비율은 $2:1$이다.

예제

1. 각 넓이 공식이 맞는지 증명하여라.¹
2. 삼차함수의 넓이 첫번째 공식에서 $\beta$가 변곡점을 지날 때, 넓이 공식을 구하여라.²

Footnotes

1. 이차함수 $f(x)=a(x-\alpha )(x-\beta )$일 때, $x$축과 둘러싸인 넓이는 $S={\int }_{\alpha }^{\beta }|a(x-\alpha )(x-\beta )|dx$ $=|a|{\int }_{\alpha }^{\beta }(x-\alpha )(\beta -x)dx$ $=|a|{\left[\frac{(\beta -\alpha )x^2}{2}-\frac{(\beta +\alpha )x^3}{3}+\frac{x^4}{4}\right]}_{\alpha }^{\beta }$ $=|a|\frac{(\beta -\alpha {)}^3}{6}$이다. ↩

2. 삼차함수 $f(x)=a(x-\alpha )(x-\beta )(x-\gamma )$이고, $\beta$가 변곡점을 지날 때, 즉, $\beta =\frac{\alpha +\gamma }{2}$일 때, $x$축과 둘러싸인 넓이는 $S={\int }_{\alpha }^{\gamma }|a(x-\alpha )(x-\beta )(x-\gamma )|dx$ $=|a|{\int }_{\alpha }^{\gamma }(x-\alpha )(\beta -x)(\gamma -x)dx$ $=|a|{\left[\frac{(\alpha +\gamma )x^3}{3}-\frac{(\alpha \gamma +{\beta }^2)x^2}{2}+\frac{\alpha \beta \gamma x}{1}-\frac{x^4}{4}\right]}_{\alpha }^{\gamma }$ $=|a|\frac{(\gamma -\alpha {)}^4}{12}$이다. ↩